Einführung und Lernziele
Contents
Einführung und Lernziele#
Bei der Datenvisualisierung geht es darum, Daten durch eine Grafik so aufzubereiten, dass Muster oder Unregelmäßigkeiten in den Daten entdeckt werden können. Dabei kann die visuelle Darstellung der Daten helfen, Muster in den Daten zu entdecken, aber sie kann auch irreführend sein. In diesem MATLAB Live Skript werden wir einen ersten Einblick in die Datenvisualisierung mit MATLAB verschaffen. Abhängig davon, wie die Art der Daten ist, die wir visualisieren wollen, gibt es verschiedene Darstellungsformen, die sogenannten Diagrammtypen. Im Folgenden betrachten wir die Diagrammtypen
Liniendiagramm,
Streudiagramm,
Balkendiagramm (Säulendiagramm),
und lernen, wann welcher Diagrammtyp zum Einsatz kommt.
Danach beschäftigen wir uns mit der Gestaltung von Diagrammtypen. Wir betrachten
Beschriftungen (Achsen, Titel, Legende),
Gitterlinien,
Marker und
Farbskalen.
Um uns zunächst das Einlesen von echten Messdaten zu ersparen, werden wir in diesem MATLAB Live Skript entweder die Graphen von mathematischen Funktionen visualisieren oder uns künstliche Messdaten per Zufallsgenerator erzeugen.
Diagramm und häufige Diagrammtypen#
Wikipedia (siehe https://de.wikipedia.org/wiki/Diagramm) definiert den Fachbegriff Diagramm folgendermaßen:
“Ein Diagramm, genannt auch (grafisches) Schaubild, ist eine grafische Darstellung von Daten, Sachverhalten oder Informationen. Je nach der Zielsetzung des Diagramms werden höchst unterschiedliche Typen eingesetzt.”
Ein in der Praxis sehr häufig eingesetzer Diagrammtyp ist das Balkendiagramm, das auch Säulendiagramm genannt wird. Das Balkendiagramm kommt zum Einsatz, wenn die Daten diskret sind. Damit ist gemeint, dass die Daten zu bestimmten Kategorien oder Mengen zugehörig sind und beispielsweise die Anzahl der Elemente oder die Häufigkeit dieser Kategorie dargestellt werden soll. Wenn Sie unsicher sind, ob die Daten diskret sind, fragen Sie sich: Kann ich den Mittelwert bilden?
Ein typisches Beispiel für ein Balkendiagramm ist die Zutatenliste für einen Obstsalat. Angenommen wir brauchen für den Obstsalat folgende Zutaten:
3 Äpfel,
2 Bananen,
4 Clementinen und
10 Datteln.
Wenn wir jetzt die Zutatenliste visualisieren wollen, können wir ein Balkendiagramm verwenden, denn man kann nicht den Mittelwert zwischen Apfel und Banane bilden. So könnte beispielsweise das zugehörige Balkendiagramm aussehen:
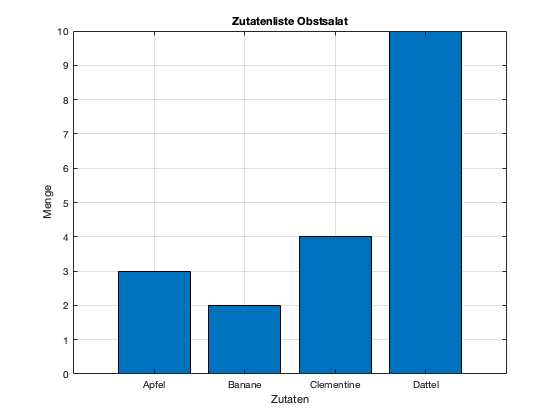
Fig. 2 Balkendiagramm für die Zutatenliste eines Obstsalates#
In der Schule kommt am häufigsten das x-y-Diagramm vor. Damit soll die Wirkung y einer Ursache x beschreiben werden. Ein typisches Beispiel ist in der Physik ein Weg-Zeit-Diagramm, bei dem die Zeit auf der x-Achse und der Weg, den ein bewegter Körper in dieser Zeit zurückgelegt hat, auf der y-Achse dargestellt wird. Auch die Schaubilder bzw. Graphen von Funktionen werden so dargestellt. Normalerweise sind die Daten au der x-Achse kontinuierlich. Vielleicht wird der zurückgelegte Weg eines Autos nur nach 1 Sekunde, 2 Sekunden, 3 Sekunden usw. gemessen. Aber dazwischen hat ist das Auto ja nicht im Nirwana verschwunden, zwischen den Werten auf der x-Achse existieren weitere Zeitpunkte, zu denen der zurückgelegte Weg ermittelt werden kann. Um diesen Unterschied zwischen Messwerten, die diskret gemessen werden, aber zu einer kontinuierlichen Größe gehören und echten kontinuierlichen Größen besser darstellen zu können, werden x-y-Diagramme als
Liniendiagramme und
Streudiagramme
dargestellt. Im Folgenden wird einmal das Zeit-Weg-Diagramm eines bewegten Körpers aufgrund der Messwerte als Streudiagramm gezeigt und einmal aufgrund der physikalischen Formel \(s=\frac{1}{2}at^2\) für eine konstante Beschleunigung von \(a=5 m/s\) als Liniendiagramm:
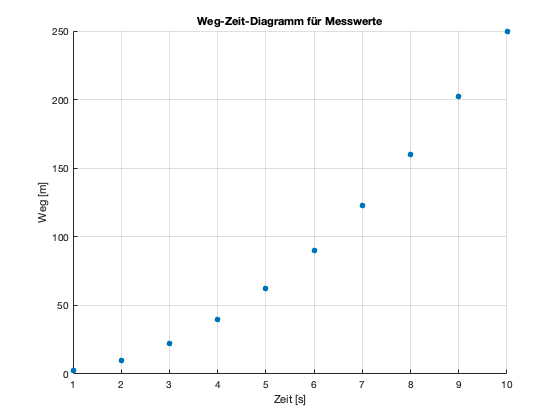
Fig. 3 Messungen Weg-Zeit eines bewegten Körpers als Streudiagramm#
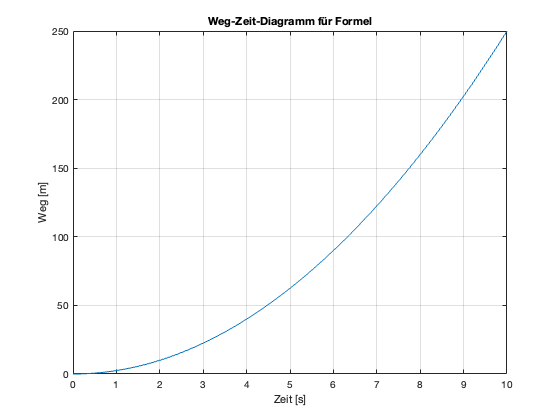
Fig. 4 Formel Weg-Zeit eines bewegten Körpers als Liniendiagramm#
Bei Messungen kann es sehr interessant sein, die Messwerte und der Messung zugrunde liegende Formel gleichzeitig zu visualisieren. Da wird erreicht, indem die Messwerte als Streudiagramm und die Formel als Liniendiagramm dargestellt wird. Damit können Ursache und Wirkung gut herausgearbeitet werden, die Güte der Messung beurteilt werden oder überhaupt neue Gesetzmäßigkeiten entdeckt werden. Für unser Weg-Zeit-Diagramm könnte das beispielsweise so aussehen:
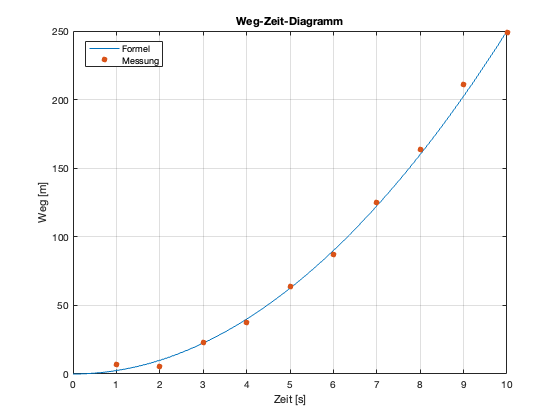
Fig. 5 Weg-Zeit-Diagramm eines bewegten Körpers (Messungen und Formel)#
Nachdem wir die drei wichtigsten Diagrammtypen kennengelernt haben, werden wir uns nun erarbeiten, wie diese in MATLAB umgesetzt werden können. Für weitere Details über Datenvisualisierung (unabhängig von Programmiersprache oder Software) empfehle ich das Buch: Datenvisualisierung - Grundlagen & Praxis von Claus O. Wilke erschienen im O’Reilly-Verlag bzw. bei dpunkt.verlag GmBH.
Exercise 46
Welchen Diagrammtyp würden Sie für die folgenden Szenarien benutzen?
Aktienkurs
Notenspiegel
Messung der Fallgeschwindigkeit zu gegebenen Höhen
Solution to Exercise 46
Aktienkurs –> Liniendiagramm
Notenspiegel –> Balkendiagramm
Messung der Fallgeschwindigkeit zu gegebenen Höhen –> Streudiagramm
Liniendiagramm zur Visualisierung von Ursache - Wirkung#
Schaubilder bzw. Graphen von Funktionen werden duch x-y-Diagramm dargestellt. Da in der Regel eine mathematische Funktion für alle x-Werte eines bestimmten Intervalles definiert wird, verwenden wir zur Darstellungen von mathematischen Funktionen das Liniendiagramm. Da MATLAB numerisch arbeitet, wird dazu eine Wertetabelle von (x,y)-Paaren angelegt. Zu jedem x-Wert wird der entsprechende y-Wert über die gegebene Funktion als \(y=f(x)\) berechnet und dann als Punkt in ein Koordinatensystem mit x- und y-Achse eingetragen. Anschließend werden die Punkte mit einer geraden Linie verbunden.
Erzeugen wir uns eine Liste mit x-Werten und dazugehörigen y-Werten als Listen.
x = [-2, -1, 0, 1, 2];
y = [4, 1, 0, 1, 4];
Um die Wertetabelle jetzt zeichnen zu lassen, bereiten wir die Grafik erst einmal vor, indem wir den Befehl figure zum Erzeugen eines Fensters ausführen, in das nachher die Grafik gezeichnet werden soll. Im interaktiven MATLAB Live Skript ist dieser Befehl optional, aber für reine MATLAB Skripte notwendig. Danach kommt die Funktion zum Zeichen der Werte als Liniendiagramm namens plot(x,y)
figure();
plot(x,y);
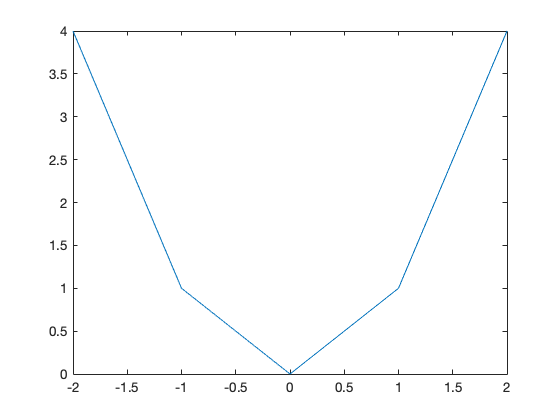
Sieht ziemlich krakelig aus. Eigentlich sollte dies eine Parabel werden im Intervall \([-2,2]\) werden. Mit nur 5 Punkten und der Tatsache, dass diese 5 Punkte mit geraden Linien verbunden werden, sieht es etwas unschön aus. Besser wird es mit mehr Punkten, aber die wollen wir jetzt nicht von Hand erzeugen.
In den vorangegangenen MATLAB Live Skripten haben wir die Erzeugungsmethode linspace() kennengelernt. Zur Erinnerung, die Funktion linspace(a,b, Anzahl) erzeugt Punkte im Intervall \([a,b]\) je nach eingestellter Anzahl.
x = linspace(-2, 2, 9);
whos x
Name Size Bytes Class Attributes
x 1x9 72 double
Der resultierende Datentyp von linspace ist ein eindimensionales Feld (1D-Array), wovon wir uns mit dem Befehl whos überzeugen könnten. Wenn wir jetzt zu jedem Element im Array das Quadrat des Elementes bilden sollen, könnten wir eine For-Schleife programmieren, die durch das eindimensionale Array geht und jedes Element quadriert. Glücklicherweise stellt MATLAB für Zahlen-Arrays, also Vektoren oder Matrizen, zusätzliche Funktionen zur Verfügung, die aus der Mathematik stammen. Wenn jedes einzelne Element eines Vektors oder einer Matrix quadriert werden soll, müssen wir den Punktoperator vor der mathematischen Operation benutzen.
y = x.^2;
disp(y)
Columns 1 through 7
4.0000 2.2500 1.0000 0.2500 0 0.2500 1.0000
Columns 8 through 9
2.2500 4.0000
Damit können wir nun wiederum ein Liniendiagramm visualisieren:
figure();
plot(x,y);
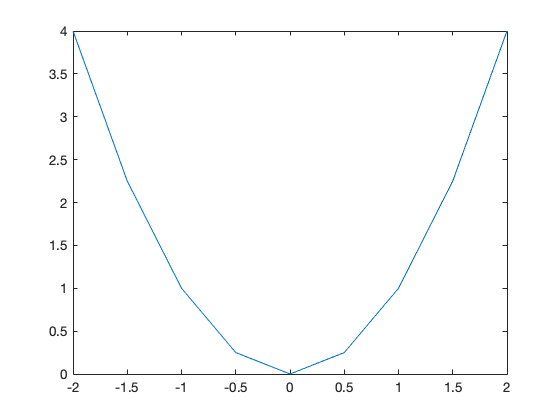
Schon besser, aber noch ein paar mehr Punkte wären noch schöner…
% Erzeugung Wertetabelle
x = linspace(-2, 2, 101);
y = x.^2;
% Visualisierung
figure;
plot(x,y);
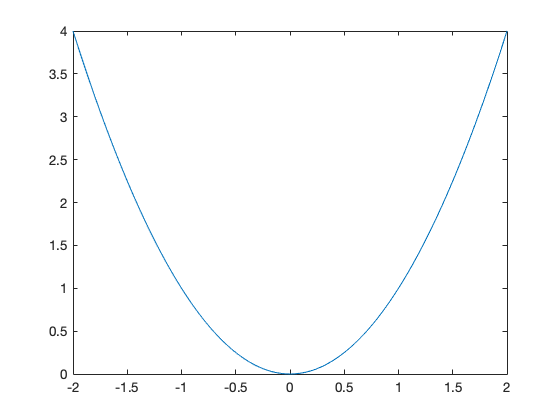
Exercise 47
Bitte plotten Sie folgende Funktionen als Liniendiagramm:
\(f(x)=7x+2\),
Sinus,
Kosinus,
Exponentialfunktion und
Wurzelfunktion.
Verändern Sie auch das Definitionsgebiet der Funktionen, also das Intervall für \(x\).
Solution to Exercise 47
% Erzeugung x-Werte
x = linspace(-3,3, 100);
% y-Werte der fünf Funktionen
y1 = 7 * x + 2;
y2 = sin(x);
y3 = cos(x);
y4 = exp(x);
y5 = sqrt(x);
% Liniendiagramm: ersetze die y-Werte jeweils durch y1, y2, ..., y5
plot(x,y1);
Beschriftung und Gitterlinien#
Ein Diagramm muss immer beschriftet sein!
Mit den Funktionen xlabel() und ylabel() beschriften Sie die x- und y-Achse.
% Erzeugung Wertetabelle
x = linspace(-10,10,200);
y = sin(x);
% Visualisierung
figure();
plot(x,y);
xlabel('Zeit in Sekunden');
ylabel('Stromstärke in Ampere');
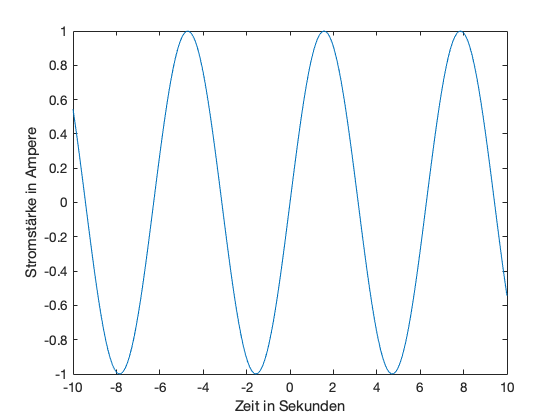
Fehlt noch ein Titel für unsere Grafik, das erledigt die Funktion title():
% Erzeugung Wertetabelle
x = linspace(-10,10,200);
y = sin(x);
% Visualisierung
figure();
plot(x,y);
xlabel('Zeit in Sekunden');
ylabel('Stromstärke in Ampere');
title('Wechselstrom');
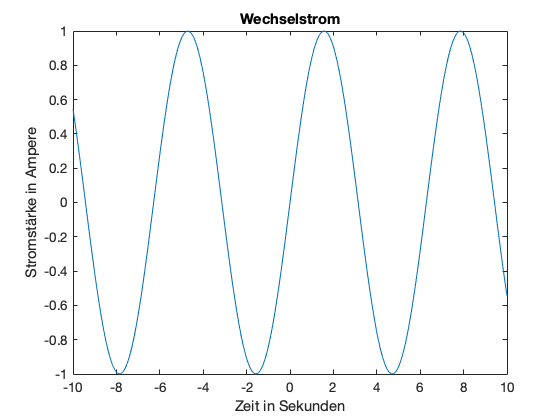
Manchmal ist es auch hilfreich, die Gitterlinien des Koordinatensystems anzeigen zu lassen, um so die Werte besser ablesen zu können. Dazu wird der Befehl grid on verwendet (grid off schaltet die Gitterlinien wieder aus):
% Erzeugung Wertetabelle
x = linspace(-10,10,200);
y = sin(x);
% Visualisierung
figure();
plot(x,y);
xlabel('Zeit in Sekunden');
ylabel('Stromstärke in Ampere');
title('Wechselstrom');
grid on;
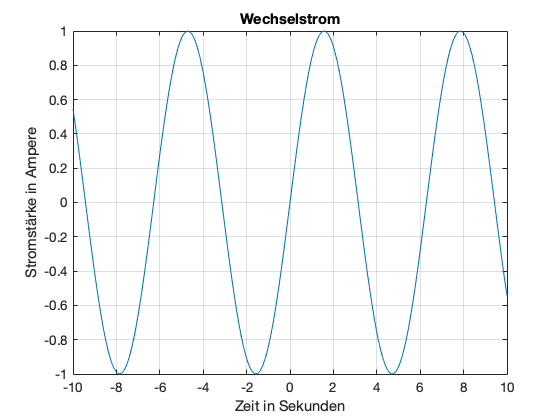
Exercise 48
Erzeugen Sie ein Weg-Zeit-Diagramm gemäß der physikalischen Formel \(s=\frac{1}{2}at^2\) mit einer konstanten Beschleunigung von \(a = 5 \frac{\text{m}}{\text{s}}\) für das Intervall \(t\in[0, 10]\) als Liniendiagramm. Beschriften Sie das Diagramm und lassen Sie die Gitterlinien anzeigen. Vergleichen Sie Ihr Ergebnis mit der dritten Grafik dieses MATLAB Live Skriptes.
Solution to Exercise 48
% Erzeugung Daten
t = linspace(0,10);
s = 0.5 * 5 .* t.^2;
% Visualisierung Daten
figure();
plot(t,s);
xlabel('Zeit [s]');
ylabel('Weg [m]');
title('Weg-Zeit-Diagramm');
grid on;
Streudiagramm zur Visualisierung von Messwerten#
Das Streudiagramm kommt vor allem bei Messungen zum Einsatz, bei denen zwar nur diskrete Daten zur Verfügung stehen, aber eigentlich von einem kontinuierlichen Ursache-Wirkungsprinzip ausgegangen wird. Außerdem kann es bei Messungen vorkommen, dass für einen x-Wert mehrere y-Werte vorkommen, weil zum Beispiel die Messung mehrfach wiederholt wurde. Daher verwenden wir für Messwerte einen neuen Diagrammtyp, das sogenannte Streudiagramm bzw. auf Englisch Scatterplot.
Die entsprechende MATLAB-Funktion heißt scatter(). Mehr Details finden Sie hier:
https://de.mathworks.com/help/matlab/ref/scatter.html
Wir erzeugen jetzt zufällige Messwerte, indem wir zu einer linearen Funktion \(f(x)=-3x+7\) eine zufällige Störung addieren. Dazu nutzen wir sogenannte normalverteilte Zufallszahlen, die über den Befehl randn(zeilen, spalten) erzeugt werden:
% Erzeugung Wertetabelle
x = [-3, -2, -1, 0, 1, 2, 3];
y = -3 .* x + 7 + randn(1,7);
Danach können wir mit dem scatter-Befehl die (x,y)-Paare zeichnen lassen:
figure();
scatter(x,y);
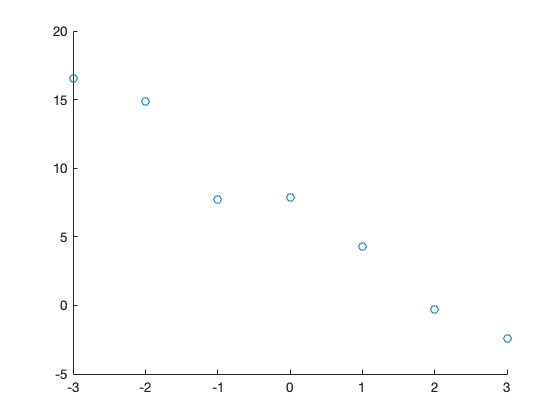
Die Befehle zur Beschriftung der Achsen, des Titels und zur Anzeige der Gitterlinien funktionieren wie gewohnt, so dass wir insgesamt den folgenden Code haben:
% Erzeugung Wertetabelle
x = [-3, -2, -1, 0, 1, 2, 3];
y = -3 .* x + 7 + randn(1,7);
% Visualisierung
figure();
scatter(x,y);
grid on;
xlabel('x');
ylabel('f(x)');
title('f(x)=-3x+7 mit normalverteilter Störung');
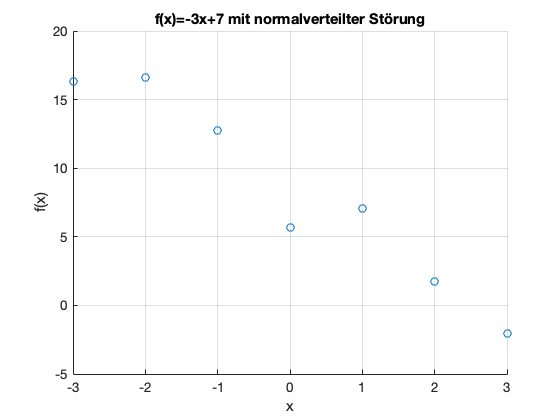
Exercise 49
Visualisieren Sie Messungen des weltweiten CO2-Ausstoßes. Die Beschreibung der Daten finden Sie hier: https://de.statista.com/statistik/daten/studie/37187/umfrage/der-weltweite-co2-ausstoss-seit-1751/ Damit Sie nicht die Daten abschreiben müssen, können Sie die nachfolgende Code-Zelle ausführen, die die Daten bereits enthält. Im x-Vektor stehen die Jahreszahlen, im y-Vektor der weltweite CO2-Ausstoß gemessen in Millionen Tonnen.
% Erzeugung Wertetabelle
x = [1960, 1965, 1970, 1975, 1980, 1985, 1990, 1995, 2000, 2005, 2010, 2011, 2012, 2013,...
2014, 2015, 2016, 2017, 2018, 2019, 2020];
y = 1.0e+04 * [0.9387, 1.1317, 1.4898, 1.7046, 1.9493, 2.0317, 2.2750, 2.3454, 2.5234, 2.9603,...
3.3343, 3.4468, 3.4974, 3.5283, 3.5534, 3.5496, 3.5452, 3.5926, 3.6646, 3.6702, 3.4807];
Beschriften Sie auch beide Achsen, setzen Sie einen Titel und lassen Sie Gitterlinien zeichnen.
Solution to Exercise 49
TODO
Zusätzliche Gestaltungsmöglichkeiten: Größe, Farbe und Symbole von Markern#
Gerade bei Messwerten ist es oft sinnvoll, zwischen Versuchsreihen zu unterscheiden. Dementsprechend bietet das Streudiagramm zahlreiche Einstellmöglichkeiten. Wir betrachten im Folgenden drei verschiedene Optionen, um Messwerte in Streudiagrammen zu visualisieren:
Größe des Markers,
Farbe des Markers und
Markersymbol.
Mit Marker ist dabei das Zeichen gemeint, mit dem die Messwerte in das Diagramm eingetagen werden.
Im folgenden Beispiel erzeugen wir sechs Lottozahlen und tragen sie in ein Streudiagramm ein. Diesmal übergeben wir der scatter()-Funktion die Größe als drittes Argument:
scatter(x,y, size).
Variieren Sie die Größe händisch mit Werten zwischen 10 und 500:
% Erzeugung Wertetabelle
x = [1, 2, 3, 4, 5, 6];
y = randi([1, 49], 1, 6);
% Visualisierung
figure();
scatter(x, y, 10);
title('Lottozahlen');
xlabel('Nummer');
ylabel('gezogene Lottozahl');
grid on;
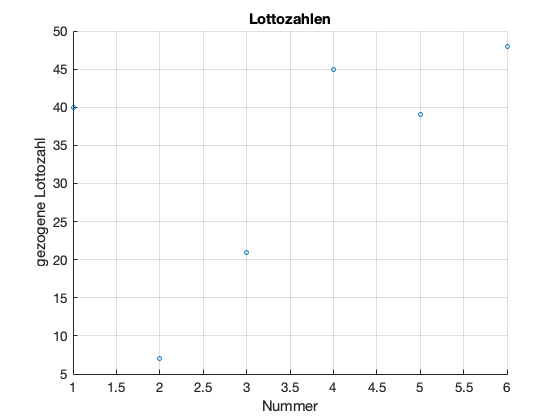
Dabei muss der dritte Parameter keine feste Zahl sein, sondern kann ebenfalls ein Vektor sein.
Exercise 50
Erzeugen Sie drei Vektoren x, y und s. x soll die Zahlen von 1 bis 10 enthalten und y soll ganzzahlige Zufallszahlen zwischen -3 und 3 enthalten. Die einzelnen Elemente \(s_i\) in s sollen nach der Formel \(s_i = 100 + 100 \cdot y_i^2\) berechnet werden. Visualisieren Sie diese Daten als Streudiagramm mit \(s\) als variable Größe.
Solution to Exercise 50
% Erzeugung der Wertetabelle
x = linspace(1, 10, 10);
y = randi([-3, 3], 1, 10);
s = 100 + 100 * y .^2; % Punktoperstor wichtig, weil elementweise quadriert wird
% Visualisierung
figure();
scatter(x, y, s);
Die Farbe des Markers wird als viertes Argument gesetzt:
scatter(x, y, size, color).
Dabei müssen die Farben in MATLAB-Syntax angegeben werden. Die Standardfarben können über ihre englischen Bezeichnungen verwendet werden:
'red', 'green', 'blue', 'cyan', 'magenta', 'yellow', 'black', 'white'
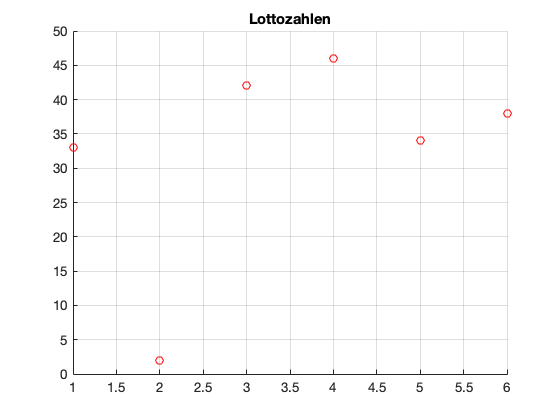
Wenn jetzt die Marker rot gefärbt werden sollen, setzen wir als viertes Argument 'red'. Manchmal möchten wir die Größe bei der Voreinstellung belassen, aber trotzdem die Farbe ändern. In diesem Fall können wir nicht einfach das dritte Argument weglassen, sondern kennzeichnen es als Standard, indem wir leere eckige Klammern als drittes Argument für die Größe verwenden.
% Erzeugung Wertetabelle
x = [1, 2, 3, 4, 5, 6];
y = randi([1, 49], 1, 6);
% Visualisierung
figure();
scatter(x, y, [], 'red');
title('Lottozahlen');
grid on;
Exercise 51
Erzeugen Sie einen Vektor mit ganzen Zahlen von 1 bis 25 (Nummern der Schüler:innen einer Klasse). Erzeugen Sie dann einen Vektor mit 25 Elementen (also Size 1x25), der zufällige Schulnoten von 1 bis 6 beinhaltet. Lassen Sie dann (Tipp: beispielsweise in einer For-Schleife) die einzelnen Noten nach dem folgenden Muster visualisieren: Wenn die Schulnote des i-ten Schülers eine 1 oder 2 ist, soll der Marker 'green' angezeigt werden, bei 3 oder 4 'yellow' und ansonsten 'red'. Visualisieren Sie die Daten als Streudiagramm.
Solution to Exercise 51
% Erzeugung Wertetabelle
x = linspace(1, 25, 25);
y = randi([1, 6], 1, 25);
% Visualisierung
figure();
hold on;
for i = 1:25
if y(i) == 1 || y(i) == 2
scatter(x(i), y(i), 'green');
elseif y(i) == 3 || y(i) == 4
scatter(x(i), y(i), 'yellow');
else
scatter(x(i), y(i), 'red');
end
end
grid on;
xlabel('Nr. Schüler:in');
ylabel('Note');
title('Notenspiegel');
% Visualisierung
figure();
scatter(x, y, [], c);
Zuletzt variieren wir noch die Marker selbst. Das folgende Bild ist ein Ausschnitt aus der MATLAB-Dokumentation und zeigt das Aussehen der verschiedenen Markersymbole und ihre Bezeichnung.
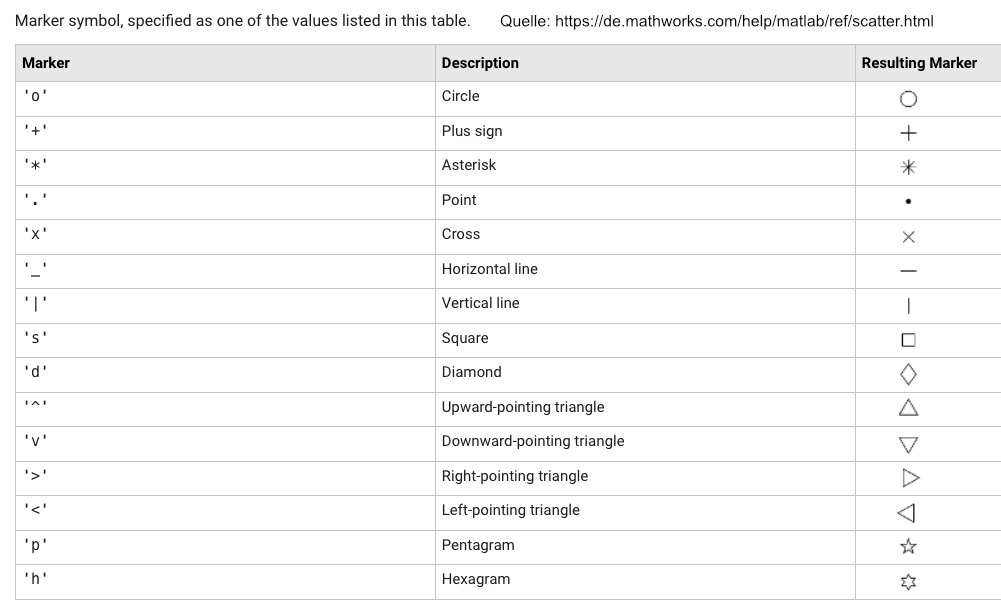
Fig. 6 Markersymbole#
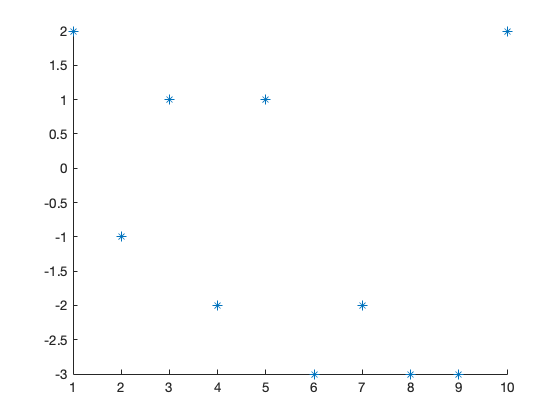
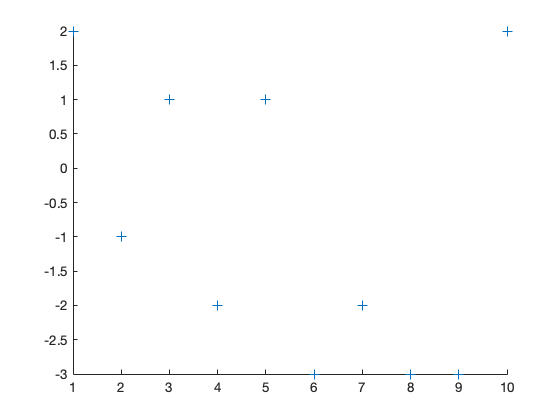
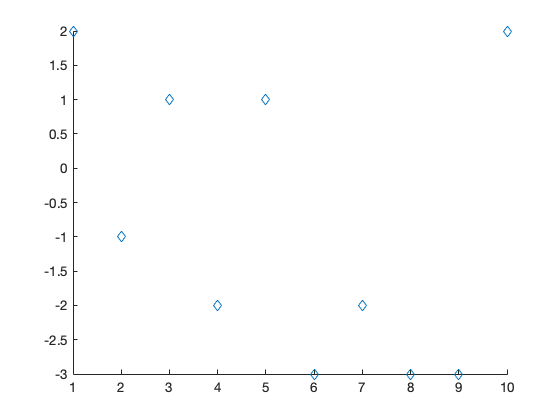
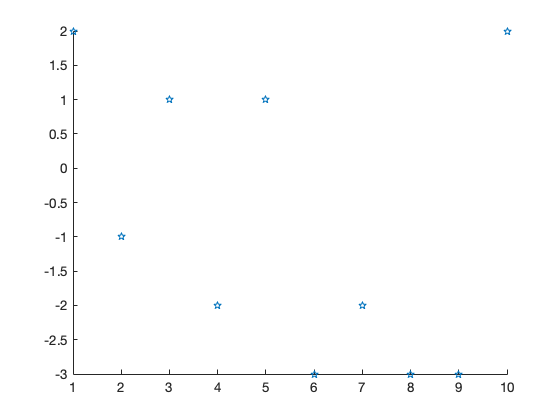
Der folgende Code zeigt Ihnen Zufallszahlen mit verschiedenen Markersymbolen:
% Erzeugung Wertetabelle
x = linspace(1, 10, 10);
y = randi([-3, 3], 1, 10);
for marker = ['*', '+', 'd', 'p']
fprintf('Jetzt kommt Markersymbol: %s', marker);
figure();
scatter(x, y, marker);
end
Jetzt kommt Markersymbol: *
Jetzt kommt Markersymbol: +
Jetzt kommt Markersymbol: d
Jetzt kommt Markersymbol: p
Mehrere Diagramme in einer Grafik#
Möchte man zwei oder gar mehrere Funktionen oder Messdaten in einer Grafik darstellen, verwendet man den plot- oder scatter-Befehl mehrfach, setzt aber den Befehl hold on; dazwischen:
% Erzeugung Wertetabelle
x = linspace(-2*pi,2*pi, 200);
y1 = sin(x);
y2 = cos(x);
% Visualisierung
figure();
plot(x,y1);
hold on;
plot(x,y2);
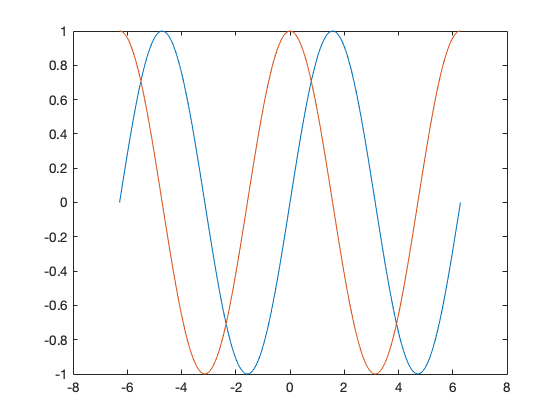
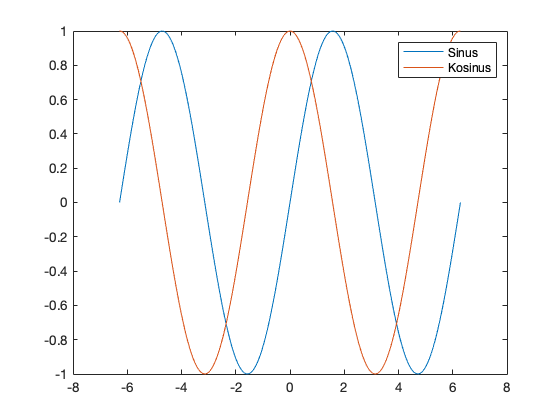
Dann ist es aber auch gut, die Kurven zu beschriften. Dazu verwendet man die Funktion legend(name1, name2, ...).
% Erzeugung Wertetabelle
x = linspace(-2*pi,2*pi, 200);
y1 = sin(x);
y2 = cos(x);
% Visualisierung
figure();
plot(x,y1);
hold on;
plot(x,y2);
legend('Sinus','Kosinus');
Exercise 52
Stellen Sie die Funktionen
\(f_1(x)=\sin(x)\),
\(f_2(x)=\sin(2x)\) und
\(f_3(x)=\sin(3x)\)
als Linien-Diagramm im Intervall \([-2\pi, 2\pi]\) dar und beschriften Sie die Kurven mit einer geeigneten Legende.
Solution to Exercise 52
% Erzeugung Wertetabelle
x = linspace(-2*pi, 2*pi);
y1 = sin(x);
y2 = sin(2*x);
y3 = sin(3*x);
% Visualisierung
figure();
plot(x, y1); hold on;
plot(x, y2);
plot(x, y3);
grid on;
title('Drei Sinusfunktionen');
legend('sin(x)', 'sin(2x)', 'sin(3x)');
Balkendiagramm zur Visualisierung von diskreten Daten / Kategorien#
Balkendiagramme oder Säulendiagramme werden zur Visualisierung von quantitativen Daten verwendet. Damit ist gemeint, dass auf der x-Achse Kategorien oder Klassen eingetragen werden, zwischen denen auch kein Mittelwert gebildet werden kann. Angenommen, wir haben folgende Daten über die beliebtesten YouTube-Streams (hier bis Mai 2021 ausgewertet) gesammelt:
YouTuber |
Song |
Anzahl der Views (in Milliarden) |
|---|---|---|
Pinkfong Kids’ Songs & Stories |
Baby Shark Dance |
8.58 |
Luis Fonsi ft. Daddy Yankee |
Despacito |
7.35 |
LooLoo Kids |
Johny Johny Yes Papa |
5.31 |
Ed Sheeran |
Shape of You |
5.31 |
Wiz Khalifa ft. Charlie Puth |
See You Again |
5.1 |
Get Movies |
Masha and the Bear: Recipe for Disaster |
4.44 |
Mark Ronson ft. Bruno Mars |
Uptown Funk |
4.18 |
Psy |
Gangnam Style |
4.06 |
Miroshka TV |
Learning Colors - Colorful Eggs on a Farm |
4.05 |
Cocomelon |
Bath Song |
4.03 |
Dann würden wir diese Daten mit einem Balkendiagramm visualisieren, weil auf der x-Achse die Namen von YouTubern stehen, also Klassen oder Kategorien und keine kontinuerlichen x-Daten.
Mit der Funktion bar() kann nun ein Balkendiagramm erstellt werden.
% Erzeugung Wertetabelle
anzahl_views = [8.58, 7.53, 5.31, 5.31, 5.1, 4.44, 4.18, 4.06, 4.05, 4.03];
% Visualisierung
figure();
bar(anzahl_views);
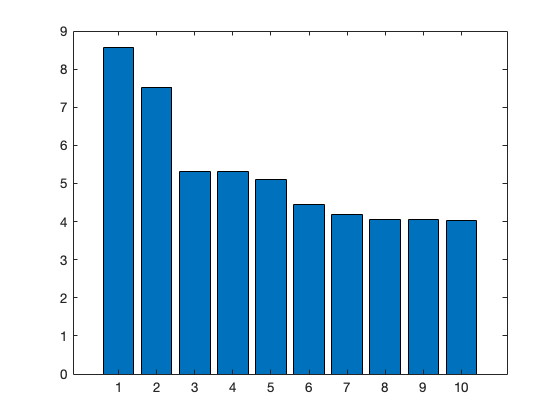
Weitere Details zu der bar()-Funktion finden Sie in der MATLAB-Dokumentation:
Schade, dass wir nur die Nummer des YouTubers ablesen können. Wenn wir anstatt der Nummern die ursprünglichen Kategorien verwenden wollen, müssen wir ein Datenobjekt mit den Kategorien erzeugen. Dazu benutzten wir die Funktion categorical( {kategorie1, kategorie2, ..., kategorieN} )
% Erzeugung Wertetabelle
youtuber = categorical({'Pinkfong', 'Lius Fonsi', 'LooLoo Kids', 'Ed Sheeran',...
'Wiz Khalifa', 'Get Movies', 'Mark Ronson', 'Psy', 'Miroshka TV', 'Cocomelon'});
anzahl_views = [8.58, 7.53, 5.31, 5.31, 5.1, 4.44, 4.18, 4.06, 4.05, 4.03];
% Visualisierung
figure();
bar(youtuber, anzahl_views);
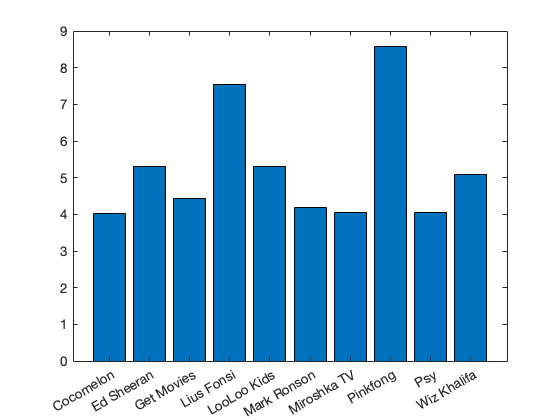
Wie Sie sehen, hat sich die Reihenfolge der Kategorien und damit der Balken geändert. In der ersten Visualisierung waren die Kategorien implizit mit 1, 2, 3, … durchnummeriert. Bei der zweiten Visualisierung, in der wir die Kategoriennamen verwendet haben, wurden die Kategorien alphabetisch sortiert. Dadurch hat sich die Reihenfolge geändert. Dies können wir verhindern, indem wir die ursprüngliche Reihenfolge wieder mit der reordercats()-Funktion erzwingen:
% Erzeugung Wertetabelle
anzahl_views = [8.58, 7.53, 5.31, 5.31, 5.1, 4.44, 4.18, 4.06, 4.05, 4.03];
youtuber = reordercats(categorical({'Pinkfong', 'Lius Fonsi', 'LooLoo Kids', 'Ed Sheeran',...
'Wiz Khalifa', 'Get Movies', 'Mark Ronson', 'Psy', 'Miroshka TV', 'Cocomelon'}) , {'Ed Sheeran', 'Pinkfong', 'Lius Fonsi', 'LooLoo Kids',...
'Wiz Khalifa', 'Get Movies', 'Mark Ronson', 'Psy', 'Miroshka TV', 'Cocomelon'});
% Visualisierung
figure();
bar(youtuber, anzahl_views);
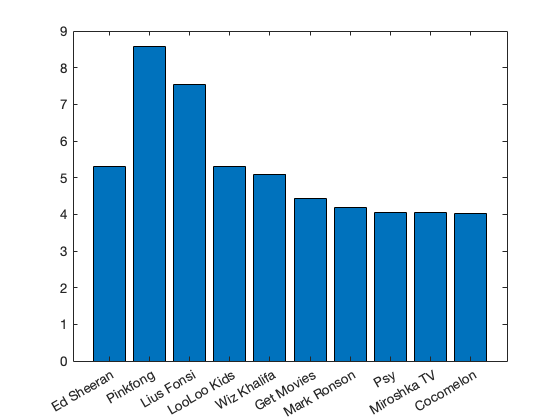
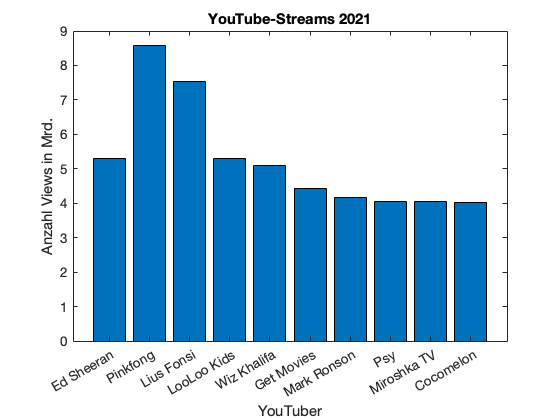
Natürlich funktionieren auch hier die Funktionen xlabel(), ylabel() und title():
figure();
bar(youtuber, anzahl_views);
xlabel('YouTuber');
ylabel('Anzahl Views in Mrd.');
title('YouTube-Streams 2021');
Exercise 53
Wie viele Semesterwochenstunden an Veranstaltungen haben Sie laut Stundenplan in diesem Semester. Visualisieren Sie die Anzahl der Stunden für jeden Wochentag in einem Balkendiagramm mit passenden Beschriftungen.
Solution to Exercise 53
% Daten
sws = [8,6,4,0,8];
woche = categorical({'Mo', 'Di', 'Mi', 'Do', 'Fr'});
woche_geordnet = reordercats(woche, {'Mo', 'Di', 'Mi', 'Do', 'Fr'});
% Visualisierung
figure();
bar(woche_geordnet, sws);
ylabel('Anzahl SWS');
title('Mein Stundenplan');
Exercise 54
Visualisieren Sie die Anzahl der Sitze, die die einzelnen Parteien bei der Bundestagswahl 2021 gewonnen haben in einem Balkendiagramm (Quelle: https://www.bundeswahlleiter.de):
CDU: 152
SPD: 206
AfD: 83
FDP: 92
DIE LINKE: 39
GRÜNE: 118
CSU: 45
Den SSW mit einem Sitz lassen Sie bitte weg. Ordnen Sie die Balken nach der aktuellen Sitzordnung im Bundestag. Ergänzen Sie passende Beschriftungen.
Solution to Exercise 54
% Daten
anzahl_sitze = [152, 206, 83, 92, 39, 118, 45];
parteien = categorical({'CDU', 'SPD', 'AfD', 'FDP', 'DIE LINKE', 'GRÜNE', 'CSU' });
parteien_geordnet = reordercats(parteien, {'DIE LINKE', 'GRÜNE', 'SPD', 'FDP', 'CDU', 'CSU', 'AfD'} );
% Visualisierung
figure();
bar(parteien_geordnet, anzahl_sitze);
xlabel('Partei');
ylabel('Anzahl Sitze');
title('Bundestagswahl 2021');
Zusammenfassung und Ausblick#
Die Visualisierung der Daten in Form von Balken- oder Streudiagrammen ist normalerweise der erste Schritt bei einer Datenanalyse. Durch die Visualisierung gewinnen wir einen ersten Eindruck darüber, ob statistische Ausreißer vorliegen oder in den Daten ein Muster erkennbar ist. Mit der Erkennung von Mustern und Gesetzmäßigkeiten in Form der linearen Regression werden wir uns im nächsten Skript beschäftigen.

