Demo Datengestütztes Prozessmangement

Das Perzeptron ist die Grundlage neuronaler Netze.

Lernziele

• Sie können das Perzeptron als mathematische Funktion formulieren und in dem Zusammenhang die folgenden Begriffe erklären:

  • gewichtete Summe (Weighted Sum),

  • Bias oder Bias-Einheit (Bias),

  • Schwellenwert (Threshold)

  • Heaviside-Funktion (Heaviside Function) und

  • Aktivierungsfunktion (Activation Function).

• Sie können das Perzeptron als ein binäres Klassifikationsproblem des überwachten Lernens einordnen.

• Sie kennen die drei Phasen, in denen ein Perzeptron trainiert wird:

  • Initialisierung der Gewichte und Festlegung der Lernrate;

  • Berechnung des prognostizierten Outputs und Aktualisierung der Gewichte sowie

  • Terminierung des Trainings.

• In Zusammenhang mit dem Training von ML-Verfahren kennen Sie die Fachbegriffe Lernrate und Epoche.

Das Perzeptron

1943 haben die Forscher Warren McCulloch und Walter Pitts das erste Modell einer vereinfachten Hirnzelle präsentiert. Zu Ehren der beiden Forscher heißt dieses Modell MCP-Neuron. Darauf aufbauend publizierte Frank Rosenblatt 1957 seine Idee einer Lernregel für das künstliche Neuron. Das sogenannte Perzeptron bildet bis heute die Grundlage der künstlichen neuronalen Netze. Inspiriert wurden die Forscher dabei durch den Aufbau des Gehirns und der Verknüpfung der Nervenzellen.

Fig. 10 Schematische Darstellung einer Nervenzelle

(Quelle: “Schematische Darstellung einer Nervenzelle” von Autor unbekannt. Lizenz: CC BY-SA 3.0)

Elektrische und chemische Eingabesignale kommen bei den Dendriten an und laufen im Zellkörper zusammen. Sobald ein bestimmter Schwellwert überschritten wird, wird ein Ausgabesignal erzeugt und über das Axon weitergeleitet. Mehr Details zu Nervenzellen finden Sie bei Wikipedia: https://de.wikipedia.org/wiki/Nervenzelle.

Eine mathematische Ungleichung ersetzt das logische Oder

Das einfachste künstliche Neuron besteht aus zwei Inputs und einem Output. Dabei sind für die beiden Inputs nur zwei Zustände zugelassen und auch der Output besteht nur aus zwei verschiedenen Zuständen. In der Sprache des maschinellen Lernens liegt also eine binäre Klassifikationsaufgabe innerhalb des Supervised Learnings vor.

Beispiel:

• Input 1: Es regnet oder es regnet nicht.

• Input 2: Der Rasensprenger ist an oder nicht.

• Output: Der Rasen wird nass oder nicht.

Den Zusammenhang zwischen Regen, Rasensprenger und nassem Rasen können wir in einer Tabelle abbilden:

Regnet es?	Ist Sprenger an?	Wird Rasen nass?
nein	nein	nein
ja	nein	ja
nein	ja	ja
ja	ja	ja

Exercise 1

Schreiben Sie ein kurzes Python-Programm, das abfragt, ob es regnet und ob der Rasensprenger eingeschaltet ist. Dann soll der Python-Interpreter ausgeben, ob der Rasen nass wird oder nicht.

# Geben Sie nach diesem Kommentar Ihren Code ein:

Solution to Exercise 1

# Eingabe
x1 = input('Regnet es (j/n)?')
x2 = input('Ist der Rasensprenger eingeschaltet? (j/n)')

# Verarbeitung
y = (x1 == 'j') or (x2 == 'j')

# Ausgabe
if y == True:
    print('Der Rasen wird nass.')
else:
    print('Der Rasen wird nicht nass.')

Für das maschinelle Lernen müssen die Daten als Zahlen aufbereitet werde, damit die maschinellen Lernverfahren in der Lage sind, Muster in den Daten zu erlernen. Anstatt “Regnet es? Nein.” oder Variablen mit True/False setzen wir jetzt Zahlen ein. Die Inputklassen kürzen wir mit x1 für Regen und x2 für Rasensprenger ab. Die 1 steht für ja, die 0 für nein. Den Output bezeichnen wir mit y. Dann lautet die obige Tabelle für das “Ist-der-Rasen-nass-Problem”:

x1	x2	y
0	0	0
1	0	1
0	1	1
1	1	1

Exercise 2

Schreiben Sie Ihren Programm-Code aus Exercise 1 um. Verwenden Sie Integer 0 und 1 für die Eingaben.

# Geben Sie nach diesem Kommentar Ihren Code ein:

Solution to Exercise 2

# Eingabe
x1 = int(input('Regnet es (ja = 1 | nein = 0)?'))
x2 = int(input('Ist der Rasensprenger eingeschaltet? (ja = 1 | nein = 0)'))

# Verarbeitung
y = (x1 == 1) or (x2 == 1)

# Ausgabe
if y == True:
    print('Der Rasen wird nass.')
else:
    print('Der Rasen wird nicht nass.')

Als nächstes ersetzen wir das logische ODER durch ein mathematisches Konstrukt: Wenn die Ungleichung

\[\omega_1 x_1 + \omega_2 x_2 \geq \theta\]

erfüllt ist, dann ist \(y = 1\) oder anders ausgedrückt, der Rasen wird nass. Und ansonsten ist \(y = 0\), der Rasen wird nicht nass. Allerdings müssen wir noch die Gewichte \(\omega_1\) und \(\omega_2\) (in Englisch: weights) geschickt wählen. Die Zahl \(\theta\) ist der griechische Buchstabe Theta und steht als Abkürzung für den sogenannten Schwellenwert (in Englisch: threshold).

Beispielsweise \(\omega_1 = 0.3\), \(\omega_2=0.3\) und \(\theta = 0.2\) passen:

• \(0.3\cdot 0 + 0.3\cdot 0 = 0.0 \geq 0.2\) nicht erfüllt

• \(0.3\cdot 1 + 0.3\cdot 0 = 0.3 \geq 0.2\) erfüllt

• \(0.3\cdot 0 + 0.3\cdot 1 = 0.3 \geq 0.2\) erfüllt

• \(0.3\cdot 1 + 0.3\cdot 1 = 0.6 \geq 0.2\) erfüllt

Exercise 3

Schreiben Sie Ihren Programm-Code aus Exercise 2 um. Ersetzen Sie das logische ODER durch die linke Seite der Ungleichung und vergleichen Sie anschließend mit \(0.2\), um zu entscheiden, ob der Rasen nass wird oder nicht.

# Geben Sie nach diesem Kommentar Ihren Code ein:

Solution to Exercise 3

# Eingabe
x1 = int(input('Regnet es (ja = 1 | nein = 0)?'))
x2 = int(input('Ist der Rasensprenger eingeschaltet? (ja = 1 | nein = 0)'))

# Verarbeitung
y = 0.3 * x1 + 0.3 * x2

# Ausgabe
if y >= 0.2:
    print('Der Rasen wird nass.')
else:
    print('Der Rasen wird nicht nass.')

Die Heaviside-Funktion ersetzt die Ungleichung

Noch sind wir aber nicht fertig, denn auch die Frage “Ist die Ungleichung erfüllt oder nicht?” muss noch in eine mathematische Funktion umgeschrieben werden. Dazu subtrahieren wir zuerst auf beiden Seiten der Ungleichung den Schwellenwert \(\theta\):

\[-\theta + \omega_1 x_1 + \omega_2 x_2 \geq 0.\]

Damit haben wir jetzt nicht mehr einen Vergleich mit dem Schwellenwert, sondern müssen nur noch entscheiden, ob der Ausdruck \(-\theta + \omega_1 x_1 + \omega_2 x_2\) negativ oder positiv ist. Bei negativen Werten, soll \(y = 0\) sein und bei positiven Werten (inklusive der Null) soll \(y = 1\) sein. Dafür gibt es in der Mathematik eine passende Funktion, die sogenannte Heaviside-Funktion (manchmal auch Theta-, Stufen- oder Treppenfunktion genannt), siehe https://de.wikipedia.org/wiki/Heaviside-Funktion.

Fig. 11 Schaubild der Heaviside-Funktion

(Quelle: “Verlauf der Heaviside-Funktion auf \(\mathbb{R}\)” von Lennart Kudling. Lizenz: gemeinfrei)

Definiert ist die Heaviside-Funktion folgendermaßen:

\[\begin{split}\Phi(x) = \begin{cases}0:&x<0\\1:&x\geq 0\end{cases}\end{split}\]

In dem Modul NumPy ist die Heaviside-Funktion schon hinterlegt, siehe

https://numpy.org/doc/stable/reference/generated/numpy.heaviside.html

Exercise 4

Visualisieren Sie die Heaviside-Funktion für das Intervall \([-3,3]\) mit 101 Punkten. Setzen Sie das zweite Argument einmal auf 0 und einmal auf 2. Was bewirkt das zweite Argument? Sehen Sie einen Unterschied in der Visualisierung? Erhöhen Sie auch die Anzahl der Punkte im Intervall. Wählen Sie dabei immer eine ungerade Anzahl, damit die 0 dabei ist.

# Geben Sie nach diesem Kommentar Ihren Code ein:

Solution to Exercise 4

import matplotlib.pylab as plt
import numpy as np

x = np.linspace(-3,3, 101)
y0 = np.heaviside(x, 0)     # an der Stelle x=0 ist y=0
y1 = np.heaviside(x, 2)     # an der Stelle x=0 ist y=2

fig, ax = plt.subplots()
ax.plot(x,y0)
ax.plot(x,y1)
ax.grid()
ax.set_title('Heaviside-Funktion');

Mit der Heaviside-Funktion können wir nun den Vergleich in der Programmverzweigung mit \(0.2\) durch eine direkte Berechnung ersetzen. Schauen Sie sich im folgenden Programm-Code an, wie wir jetzt ohne logisches Oder und ohne Programmverzweigung if-else auskommen:

# Import der notwendigen Module
import numpy as np

# Eingabe
x1 = int(input('Regnet es (ja = 1 | nein = 0)?'))
x2 = int(input('Ist der Rasensprenger eingeschaltet? (ja = 1 | nein = 0)'))

# Verarbeitung
y = np.heaviside(0.3 * x1 + 0.3 * x2, 1.0)

# Ausgabe
ergebnis_als_text = ['Der Rasen wird nass.', 'Der Rasen wird nicht nass.']
print(ergebnis_als_text[int(y)])

Das Perzeptron mit mehreren Eingabewerten

Das Perzeptron für zwei Eingabewerte lässt sich in sehr natürlicher Weise auf viele Eingabewerte verallgemeinern.

Wenn wir nicht nur zwei, sondern \(n\) Eingabewerte \(x_i\) haben, brauchen wir entsprechend auch \(n\) Gewichte \(\omega_i\). Die Eingabewerte können wir in einem Spaltenvektor zusammenfassen, also

\[\begin{split}\mathbf{x} = \begin{pmatrix} x_1 \\ x_2 \\ \vdots \\ x_n \end{pmatrix}.\end{split}\]

Auch die Gewichte können wir in einem Spaltenvektor zusammenfassen, also

\[\begin{split}\boldsymbol{\omega} = \begin{pmatrix} \omega_1 \\ \omega_2 \\ \vdots \\ \omega_n\end{pmatrix}\end{split}\]

schreiben. Nun lässt sich die Ungleichung recht einfach durch das Skalarprodukt abkürzen:

\[\boldsymbol{\omega}^{T}\mathbf{x} = \omega_1 x_1 + \omega_2 x_2 + \ldots + \omega_n x_n \geq \theta.\]

Wie bei dem Perzeptron mit zwei Eingängen wird der Schwellenwert \(\theta\) durch Subtraktion auf die linke Seite gebracht. Wenn wir jetzt bei dem Vektor \(\boldsymbol{\omega}\) mit den Gewichten vorne den Vektor um das Element \(\omega_0 = -\theta\) ergänzen und den Vektor \(\mathbf{x}\) mit \(x_0 = 1\) erweitern, dann erhalten wir

\[\boldsymbol{\omega}^{T}\mathbf{x} = -\theta \cdot 1+ \omega_1 x_1 + + \omega_2 x_2 + \ldots + \omega_n x_n \geq 0.\]

Genaugenommen hätten wir jetzt natürlich für die Vektoren \(\boldsymbol{\omega}\) und \(\mathbf{x}\) neue Bezeichnungen einführen müssen, aber ab sofort gehen wir immer davon aus, dass die mit dem negativen Schwellenwert \(-\theta\) und \(1\) erweiterten Vektoren gemeint sind. Der negative Schwellenwert wird übrigens in der ML-Community Bias oder Bias-Einheit (Bias Unit) genannt.

Um jetzt klassfizieren zu können, wird auf die gewichtete Summe \(\boldsymbol{\omega}^{T}\mathbf{x}\) die Heaviside-Funktion angewendet. Manchmal wird anstatt der Heaviside-Funktion auch die Signum-Funktion verwendet. Im Folgenden nennen wir die Funktion, die auf die gewichtete Summe angewendet wird, Aktivierungsfunktion.

Definition 1

Das Perzeptron ist ein künstliches Neuron mit Gewichten \(\boldsymbol{\omega}\) und einem Schwellenwert \(\theta\). Das Perzeptron berechnet eine gewichtete Summe der Inputs \(\mathbf{x}\in\mathbb{R}^n\) und wendet dann eine Aktivierungsfunktion \(\Phi\) an, um den Output \(y\) zu berechnen:

\[y = \Phi(\boldsymbol{\omega}^{T}\mathbf{x}) = \Phi(-\theta + \omega_1 x_1 + \ldots + \omega_n x_n).\]

Eine typische Visualisierung des Perzeptrons ist in der folgenden Abbildung Schematische Darstellung eines Perzeptrons gezeigt. Die Inputs und der Bias werden durch Kreise symbolisiert. Die Multiplikation der Inputs \(x_i\) wird durch Kanten dargestellt, die mit den Gewichten \(\omega_i\) beschriftet sind. Die einzelnen Summanden \(\omega_i x_i\) treffen sich sozusagen im mittleren Kreis, wo auf die gewichtete Summe dann eine Aktivierungsfunktion angewendet wird. Das Ergebnis, der Output \(y\) wird dann berechnet und wiederum als Kreis gezeichnet.

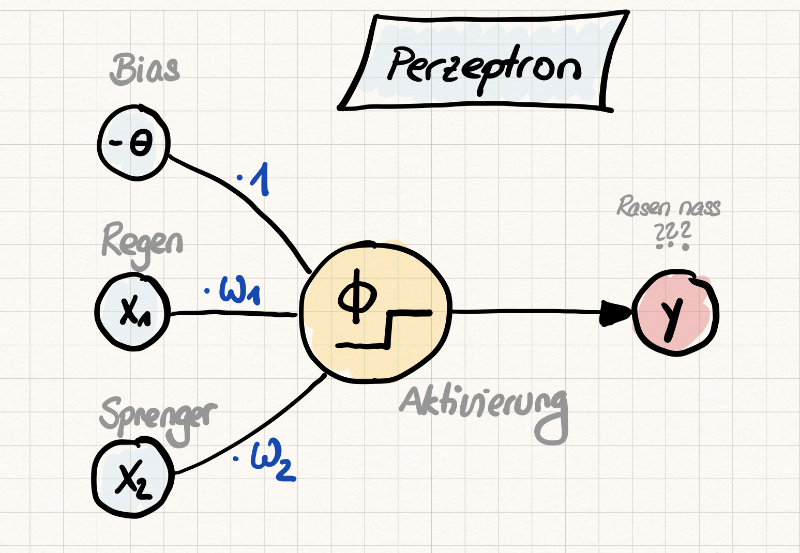
Fig. 12 Schematische Darstellung eines Perzeptrons

Hebbsche Regel

Kaum zu glauben, aber die Idee zum Lernen der Gewichte eines Perzeptrons stammt nicht von Informatiker:innen, sondern von einem Psychologen namens Donald Olding Hebb. Im Englischen wird seine Arbeit meist durch das Zitat

“what fires together, wires together”

kurz zusammengefasst. Hebb hat die Veränderung der synaptischen Übertragung von Neuronen untersucht und dabei festgestellt, dass je häufiger zwei Neuronen gemeinsam aktiv sind, desto eher werden die beiden aufeinander reagieren.

Die Hebbsche Regel wird beim maschinellen Lernen dadurch umgesetzt, dass der Lernprozess mit zufälligen Gewichten startet und dann der prognostizierte Output mit dem echten Output verglichen wird. Je nachdem, ob der echte Output erreicht wurde oder nicht, werden nun die Gewichte und damit der Einfluss eines einzelnen Inputs verstärkt oder nicht. Dieser Prozess - Vergleichen und Abändern der Gewichte - wird solange wiederholt, bis die passenden Gewichte gefunden sind.

Als Formel wird die Lernregel folgendermaßen formuliert:

\[\omega_i^{\text{neu}} = \omega_i^{\text{aktuell}} + \alpha \cdot(y - \hat{y}^{\text{aktuell}}) \cdot x_i.\]

Dabei gehen wir davon aus, dass das Perzeptron \(m\) Inputs mit der Bezeichnung \(x_i\) und eine Bias-Einheit \(x_0=1\) hat. Der Output ist hier mit \(y\) gekennzeichnet. Wir berechnen nun, welchen Output \(\hat{y}^{\text{aktuell}}\) das Perzeptron mit den aktuellen Gewichten \((\omega_0^{\text{aktuell}}, \omega_1^{\text{aktuell}}, \ldots, \omega_m^{\text{aktuell}})\) prognostizieren würde. Dann vergleichen wir diesen Output mit dem echten Output \(y\).

• Wenn jetzt der echte Output größer ist als der Wert, den unser Perzeptron prognostiziert, dann ist \(y - \hat{y}^{\text{aktuell}} > 0\). Indem wir nun zu den alten Gewichten den Term \( \alpha \cdot(y - \hat{y}^{\text{aktuell}})\) addieren, verstärken wir die alten Gewichte. Dabei berücksichtigen wir, ob der Input überhaupt einen Beitrag zum Output liefert, indem wir zusätzlich mit \(x_i\) multiplizieren. Ist nämlich der Input \(x_i=0\), wird so nichts an den Gewichten geändert.

• Ist jedoch der echte Output kleiner als der prognostizierte Output, dann ist \(y - \hat{y}^{\text{aktuell}} < 0\). Daher werden nun die alten Gewichte durch die Addition des negativen Terms \(\alpha \cdot(y - \hat{y}^{\text{aktuell}})\cdot x_i\) abgeschwächt.

Damit die Schritte zwischen der Abschwächung und der Verstärkung nicht zu groß werden, werden sie noch mit einem Vorfaktor \(\alpha\) multipliziert, der zwischen 0 und 1 liegt. Ein typischer Wert von \(\alpha\) ist \(0.0001\). Dieser Vorfaktor \(\alpha\) wird Lernrate genannt.

Perzeptron-Training am Beispiel des logischen ODER

Das logische Oder ist bereits durch die Angabe der folgenden vier Datensätzen komplett definiert:

x0	x1	x2	y
1	0	0	0
1	0	1	1
1	1	0	1
1	1	1	1

Im Folgenden wird das Training eines Perzeptrons Schritt für Schritt vorgerechnet.

Schritt 1: Initialisierung der Gewichte und der Lernrate

Wir brauchen für die drei Inputs drei Gewichte und setzen diese drei Gewichte jeweils auf 0. Wir sammeln die Gewichte als Vektor, also

\[\vec{\omega}^{T} = (\omega_0, \omega_1, \omega_2) = (0, 0, 0).\]

Darüber hinaus müssen wir uns für eine Lernrate \(\alpha\) entscheiden. Obwohl normalerweise ein kleiner (aber positiver) Wert gewählt wird, setzen wir der Einfachheit halber die Lernrate auf 1, also \(\alpha = 1\).

Schritt 2: Berechnung des Outputs und ggf. Anpassung der Gewichte

Wir setzen nun solange nacheinander den ersten, zweiten, dritten und vierten Trainingsdatensatz in die Berechnungsvorschrift unseres Perzeptrons ein, bis die Gewichte für alle vier Trainingsdatensätze zu einer korrekten Prognose führen. Zur Erinnerung, wir berechnen den aktuellen Output des Perzeptrons mit der Formel

\[\hat{y}^{aktuell} = \Phi(\boldsymbol{\omega}^{T}\mathbf{x}) = \Phi(\omega_0 x_0 + \omega_1 x_1 + \omega_2 x_2).\]

Schritt 3: Terminierung

Die letzten vier Iterationen mit den Gewichten \((-1,1,1)\) prognostizierten jeweils das richtige Ergebnis. Daher können wir nun mit den Iterationen stoppen.

Zusammenfassung und Ausblick

In diesem Kapitel haben wir die Theorie des Perzeptrons kennengelernt. Als nächstes beschäftigen wir uns damit, wie wir mit dem in Scikit-Learn implementierten Perzeptron handgeschriebene Ziffern klassifizieren.