4.3 Zufallszahlen

In diesem Kapitel werden wir uns mit der Erzeugung und Anwendung von Zufallszahlen in Python beschäftigen. Wir nutzen dazu das Modul numpy.random aus der Bibliothek NumPy.

Lernziele

Lernziele

• Sie kennen das Modul numpy.random.

• Sie können mit .randint() gleichverteilte Integers und mit .uniform() gleichverteilte Floats erzeugen lassen.

• Sie können mit .normal() normalverteilte Floats zu einem vorgegebenen Mittelwert und einer vorgegebenen Standabweichung erzeugen lassen.

• Sie kennen den Unterschied zwischen gleichverteilten und normalverteilten Zufallszahlen.

Gleichverteilte Zufallszahlen

Beim Würfeln mit einem sechseitigen Würfel (W6) hat jede Augenzahl von 1 bis 6 die gleiche Wahrscheinlichkeit von 1/6. Wenn wir mit Python einen solchen Würfel simulieren möchten, können wir die Funktion randint() aus dem Modul numpy.random verwenden. Dazu müssen wir zunächst NumPy importieren.

import numpy as np

wuerfelwurf = np.random.randint(1, 7)
print(wuerfelwurf)

2

Die Funktion randint() kann nicht ohne Argumente aufgerufen werden, denn wir müssen den Bereich vorschreiben, aus dem die gleichverteilten Zufallszahlen gezogen werden sollen. Der Bereich wird durch das erste und zweite Argument der Funktion gebildet, wobei das erste Argument inklusive ist und das zweite Argument exklusive. Da das erste Argument inklusiv ist, geben wir hier die 1 an. Dahingegen müssen wir als zweites Argument die 7 übergeben, um gleichverteilte Zufallszahlen bis 6 zu bekommen, da das zweite Argument exklusiv ist.

Wir können auch ein drittes Argument übergeben, das die Anzahl der gezogenen Zufallszahlen steuert. Mit dem folgenden Code werden beispielsweise 10 gleichverteilte Integers zwischen 1 und 6 zufällig gezogen.

wuerfelwurfe = np.random.randint(1, 7, 10)
print(wuerfelwurfe)

[4 6 6 1 1 3 5 4 3 6]

Probieren wir das neu erlernte Wissen in einer Mini-Übung aus.

Mini-Übung

Lassen Sie sechs Lottozahlen erzeugen, d.h. sechs Integer, die zwischen 1 und 49 gleichmäßig verteilt sind. Die Lottozahlen sollen auch ausgegeben werden.

Könnte damit die Ziehung der Lottozahlen simuliert werden?

# Hier Ihr Code

Lösung

import numpy as np

# Erzeugung der Lottozahlen
lottozahlen = np.random.randint(1, 50, 6)

# Ausgabe
print(lottozahlen)

Eine Simulation der Ziehung der Lottozahlen ist damit nicht möglich. Bei der echten Ziehung darf jede Zahl nur einmal vorkommen, dies gewährleistet der obige Code nicht.

Sollen gleichverteilte Floats erzeugt werden, nutzen wir die Funktion .uniform(), die ebenfalls im Modul numpy.random enthalten ist. Hier können wir scheinbar auf die Angabe eines Bereichs verzichten.

zufallszahl = np.random.uniform()
print(zufallszahl)

0.3430968975040134

Wenn wir die obige Code-Zelle mehrfach ausführen, stellen wir fest, dass die gleichverteilten Floats zwischen 0 und 1 liegen. Etwas präziser formuliert liegen die Zufallszahlen in dem halboffenen Intervall \([0, 1)\). Wir können auch hier das Intervall vorschreiben, indem wir die linke Intervallgrenze als erstes Argument (inklusiv) übergeben und die rechte Intervallgrenze als zweites Argument (exklusiv).

zufallszahl = np.random.uniform(-5.2, 3.0)
print(zufallszahl)

-2.956786827978762

Mit Hilfe des dritten Argumentes können wir mehreren Zufallszahlen gleichzeitig erzeugen lassen.

zufallszahlen = np.random.uniform(10, 20, 5)
print(zufallszahlen)

[17.68010453 12.33589078 11.62338006 12.58245081 16.05073857]

Damit werden fünf gleichverteilte Zufallszahlen zwischen 10 und 20 (exklusiv) generiert.

Wir wollen nun analysieren, ob die Zufallszahlen wirklich gleichmäßig aus dem Intervall \([10, 20)\) stammen. Dazu lassen wir 1000 gleichverteilte Zufallszahlen generieren. Danach teilen wir das Intervall in 10 Abschnitte und lassen nun von \([10, 11)\), \([11, 12)\), \([12, 13)\) usw. bis \([19, 20)\) zählen, wie häufig eine Zufallszahl aus diesem Teilintervall kommt. Dieses sogenannte Histogramm sieht folgendermaßen aus (den Code brauchen Sie noch nicht verstehen, das kommt später).

import matplotlib.pyplot as plt

zufallszahlen = np.random.uniform(10, 20, 2000)

plt.hist(zufallszahlen)
plt.title('Histogramm: Gleichverteilung im Intervall [10, 20]')
plt.xlabel('Teilintervalle')
plt.ylabel('Häufigkeit');

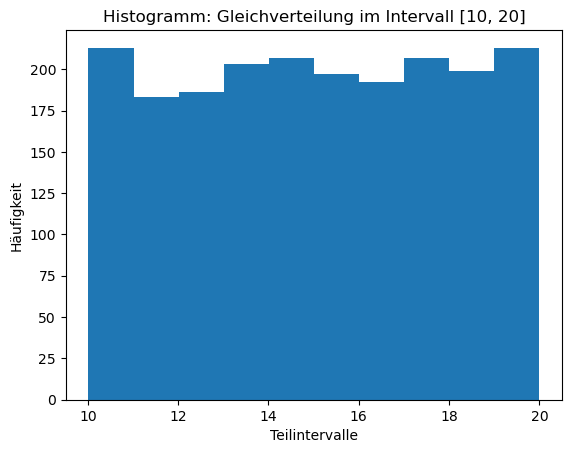
Ordnet man die gezogenen Zufallszahlen den 10 Teilintervallen zu, so sind in jedem Teilintervall ungefähr 200 Zufallszahlen enthalten.

Normalverteilte Zufallszahlen

Eine normalverteilte Zufallszahl folgt der sogenannten Normalverteilung oder Gaußschen Verteilung. Das ist eine Wahrscheinlichkeitsverteilung, die durch ihr Glockenkurven-Diagramm bekannt ist. Sie ist eine der wichtigsten Modelle in Natur- und Ingenieurwissenschaften, da viele Messgrößen (z. B. Körpergröße, Fertigungstoleranzen, Messfehler) näherungsweise normalverteilt sind.

Die Normalverteilung wird durch zwei Parameter beschrieben: den Mittelwert (oder Erwartungswert) und die Standardabweichung. Der Mittelwert ist der Wert, um den die Werte im Durchschnitt zentriert sind. Die Standardabweichung ist ein Maß für die Streuung der Werte.

In Python können wir mit der Funktion numpy.random.normal() normalverteilte Zufallszahlen erzeugen:

zufallszahl = np.random.normal(0, 1)
print(zufallszahl)

-0.4232461933689737

Das erste Argument 0 steht für einen Mittelwert von 0. Das zweite Argument 1 bedeutet, dass die Normalverteiung eine Standardabweichung von 1 hat.

Wir können auch mehrere Zahlen gleichzeitig erzeugen:

zufallszahlen = np.random.normal(0, 1, 5)
print(zufallszahlen)

[-1.09411153  0.44373465 -0.83986601  3.10657827 -2.0308883 ]

Jetzt wurden fünf normalverteilte Zufallszahlen erzeugt.

Mini-Übung

Bei einer Schulklasse wird die Körpergröße der Jugendlichen (Alter: 14 bis 18 Jahre) gemessen. Der Mittelwert bei den Mädchen ist 166.3 cm (Standardabweichung 6.39 cm) und bei den Jungen 176.8 cm (Standardabweichung 7.46 cm) (Quelle: Wikipedia).

Lassen Sie die Körpergrößen einer durchschnittlichen Schulklasse (= 13 Mädchen und 13 Jungen) erzeugen und ausgeben.

# Hier Ihr Code

Lösung

import numpy as np

# Erzeugung der Körpergrößen
maedchen = np.random.normal(166.3, 6.39, 13)
jungen = np.random.normal(176.8, 7.46, 13)

# Ausgabe
print(maedchen)
print(jungen)

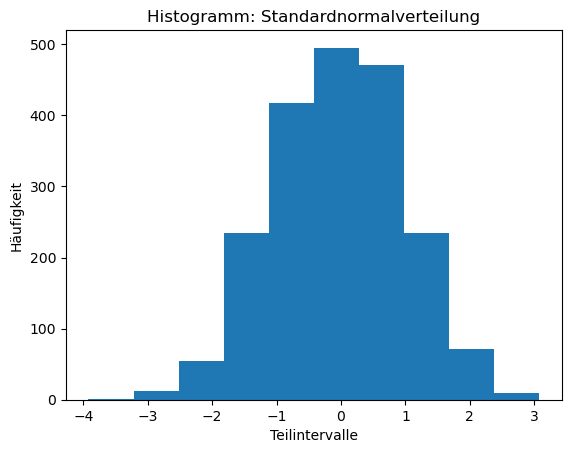
Auch hier wollen wir visualisieren, wie die Häufigkeit der Zufallszahlen verteilt ist. Dazu erzeugen wir 2000 normalverteilte Zufallszahlen mit Mittelwert 0 und Standardabweichung 1, was standardnormalverteilt genannt wird. Diesmal nehmen wir 10 automatische Teilintervalle, um die Häufigkeiten der Zufallszahlen pro Teilintervall anzeigen zu lassen.

import matplotlib.pyplot as plt

zufallszahlen = np.random.normal(0, 1, 2000)

plt.hist(zufallszahlen)
plt.title('Histogramm: Standardnormalverteilung')
plt.xlabel('Teilintervalle')
plt.ylabel('Häufigkeit');

Zusammenfassung und Ausblick

Mit den Zufallszahlen können wir Anwendungen des Alltags durch Python simulieren lassen. Bevor wir sie einsetzen, müssen wir jedoch entscheiden, ob wir Integers oder Floats benötigen und ob sie gleichverteilt oder normalverteilt sein sollen. Das nächste Kapitel führt Kontrollstrukturen ein, um abhängig von einer Bedingung Code auszuführen.