12.3 DataFrames visualisieren#
Bisher haben wir die Daten für die Visualisierung manuell erzeugt. In diesem Kapitel beschäftigen wir uns damit, wie Pandas-DataFrames professionell visualisiert werden. Wir lernen fortgeschrittene Techniken kennen, die beispielsweise für das Anfertigen einer Bachelorarbeit wichtig sind.
Lernziele#
Lernziele
Sie können den Zeilenindex .index und den Spaltenindex .columns aus einem DataFrame extrahieren.
Sie können den Text der Achsenbeschriftung drehen.
Sie können mit axhline() und axvline() Referenzlinien zu Plots hinzufügen.
Sie können Subplots für komplexere Visualisierungen erstellen.
Sie können Korrelationsanalysen graphisch aufbereiten.
Sie können Plots für Bachelorarbeiten und Präsentationen optimieren.
Visualisierung von DataFrames#
Aber wie kombinieren wir jetzt die Funktionalitäten des Pandas-Moduls mit denen des Matplotlib-Moduls? Der grundlegende Datentyp für Matplotlib ist das NumPy-Array und auch in den Pandas-Datenobjekten stecken im Kern NumPy-Arrays. Daher funktionieren die Plotting-Funktionalitäten von Matplotlib direkt. Wünschenswert wäre allerdings, den Zeilen- oder den Spaltenindex für die Beschriftung zu nehmen. Beides ist in dem DataFrame-Objekt abgespeichert. Wir können mit
.indexauf den Zeilenindex und.columnsauf den Spaltenindex
zugreifen. Die Methode .to_numpy() liefert die Werte in der Tabelle als
NumPy-Array zurück. Das brauchen wir für die Visualisierung jedoch nicht, denn die
Tabellendaten können direkt visualisiert werden.
Wir verwenden einen realistischen Datensatz und importieren den uns schon bekannten Datensatz der Top7-Fußballvereine der Bundesliga 2020/21 (→ Download). Dann lassen wir den Zeilen- und Spaltenindex direkt anzeigen:
import pandas as pd
import numpy as np
data = pd.read_csv('bundesliga_top7_offensive.csv', index_col=0)
print('Zeilenindex: ')
print(data.index)
print('\nSpaltenindex:')
print(data.columns)
Zeilenindex:
Index(['Manuel Neuer', 'Thomas Müller', 'David Alaba', 'Jérôme Boateng',
'Robert Lewandowski', 'Joshua Kimmich', 'Kingsley Coman',
'Benjamin Pavard', 'Alphonso Davies', 'Serge Gnabry',
...
'Petar Musa', 'Florian Hübner', 'Cedric Teuchert', 'Keita Endo',
'Niko Gießelmann', 'Loris Karius', 'Akaki Gogia', 'Leon Dajaku',
'Tim Maciejewski', 'Joshua Mees'],
dtype='object', name='Name', length=177)
Spaltenindex:
Index(['Club', 'Nationality', 'Position', 'Age', 'Matches', 'Starts', 'Mins',
'Goals', 'Assists', 'Penalty_Goals', 'Penalty_Attempted', 'xG', 'xA',
'Yellow_Cards', 'Red_Cards'],
dtype='object')
Nun können wir die Daten aus dem Pandas-DataFrame extrahieren und visualisieren.
Wenn wir beispielsweise wissen wollen, wie alt die Spieler der Eintracht
Frankfurt sind, filtern wir zuerst nach Eintracht Frankfurt. Dann speichern wir
die Namen der Spieler mit dem Zeilenindex in der Variablen x und das Alter
Age in y.
# Daten filtern
data_eintracht_frankfurt = data.loc[ data['Club'] == 'Eintracht Frankfurt' ]
x = data_eintracht_frankfurt.index
y = data_eintracht_frankfurt['Age']
Da es sich bei den Spielern um Kategorien, also diskrete Daten handelt,
verwenden wir ein Balkendiagramm zur Visualisierung. Für eine ansprechende
Darstellung nutzen wir ein vordefiniertes Theme, das wir über matplotlib.style
importieren.
import matplotlib.pyplot as plt
# vordefiniertes Styling-Theme auswählen z.B. 'ggplot', 'seaborn-v0_8', 'dark_background'
import matplotlib.style as style
style.use('seaborn-v0_8')
# Visualisierung
plt.figure()
plt.bar(x, y)
plt.xlabel('Spieler')
plt.ylabel('Alter')
plt.title('Spielerdaten Eintracht Frankfurt 20/21')
# Rotation der x-Achsenbeschriftung um 45 Grad mit rechtsbündiger Ausrichtung
plt.xticks(rotation=45, ha='right')
plt.tight_layout()
plt.show()
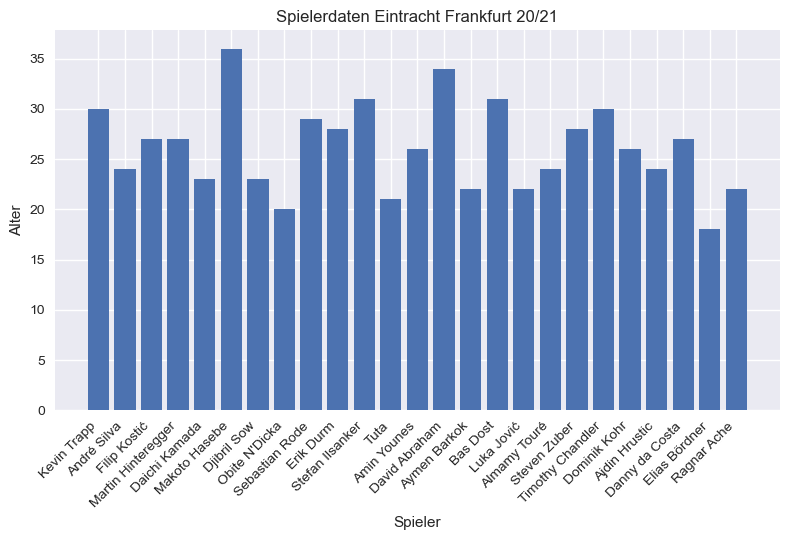
Die Funktion xticks() manipuliert die Beschriftung der x-Achse. Im obigen
Code-Beispiel wird der Beschriftungstext um 45 Grad gedreht und rechtsbündig
ausgerichtet. tight_layout() führt zu weniger Abständen zwischen dem Plot der
umgebenden Zeichenfläche.
Referenzlinien hinzufügen#
Als nächstes möchten wir in den Plot Zusatzinformationen einblenden. So würden wir gerne hervorheben, wo das Durchschnittsalter der Fußballspieler liegt. Dadurch können wir schnell ablesen, welcher Spieler über dem Durchschnitt liegt und welcher jünger als der Durchschnitt ist.
Dazu müssen wir zunächst die Zusatzinformation, in diesem Beispiel den Mittelwert, aus den Daten berechnen.
mittelwert_alter = data_eintracht_frankfurt['Age'].mean()
print(f'Mittleres Alter der Spieler: {mittelwert_alter:.1f} Jahre')
Mittleres Alter der Spieler: 26.1 Jahre
Nun ergänzen wir den Plot der Altersangaben mit dem Mittelwert. Wir zeichnen
eine horizontale Linie mit der Höhe des Altersdurchschnitts. Dazu verwenden wir
die Funktion axhline(). Für vertikale Linien gibt es entsprechend axvline().
Zusätzlich fügen wir mit legend() eine Legende ein, um zu erklären, welche
Bedeutung die Linie hat. Das sogenannte Label, also die Beschriftung der
Legende, wir zuvor als Argument in axhline() übergeben. Auch die Formatierung
der Linie mit roter Farbe color='red', der Linienstil linestyle='--' und die
Linienbreite linewidth=2 werden an dieser Stelle als Argumente eingefügt, so
dass wir insgesamt den folgenden Plot erhalten:
# Daten
x = data_eintracht_frankfurt.index
y = data_eintracht_frankfurt['Age']
# Visualisierung
plt.figure()
plt.bar(x, y)
plt.xlabel('Spieler')
plt.ylabel('Alter')
plt.title('Spielerdaten Eintracht Frankfurt 20/21')
# Rotation der x-Achsenbeschriftung um 45 Grad mit rechtsbündiger Ausrichtung
plt.xticks(rotation=45, ha='right')
# Horizontale Linie für den Mittelwert
plt.axhline(mittelwert_alter, color='red', linestyle='--', linewidth=2,
label=f'Durchschnittsalter: {mittelwert_alter:.1f} Jahre')
plt.legend()
plt.tight_layout()
plt.show()
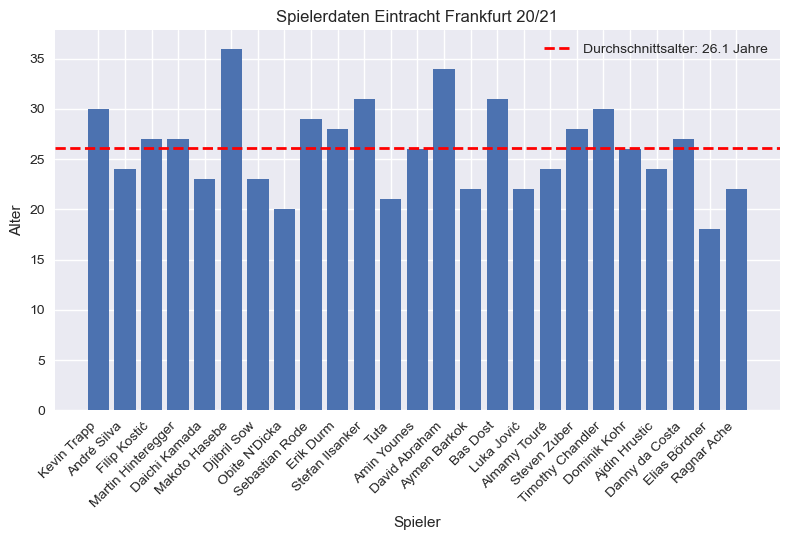
Mini-Übung
Berechnen Sie jetzt den Mittelwert der Minuten, die ein Spieler der Eintracht Frankfurt durchschnittlich im Einsatz war. Erstellen Sie ein Balkendiagramm der Spielzeiten und ergänzen Sie eine horizontale schwarze Linie für den Mittelwert.
# Hier Ihr Code
Lösung
x = data_eintracht_frankfurt.index
y = data_eintracht_frankfurt['Mins']
min_durchschnitt = y.mean()
# Visualisierung
plt.figure()
plt.bar(x, y)
plt.axhline(min_durchschnitt, color='black', linestyle='--', linewidth=2,
label=f'Durchschnitt: {min_durchschnitt:.0f} Min')
plt.xlabel('Spieler')
plt.ylabel('Minuten')
plt.title('Spielzeiten Eintracht Frankfurt 20/21')
plt.xticks(rotation=45, ha='right')
plt.legend()
plt.tight_layout()
plt.show()
Subplots für komplexere Darstellungen#
Hier sehen wir eine wichtige Erweiterung zu den bisherigen Plots: Subplots ermöglichen es uns, mehrere Diagramme nebeneinander in einer Abbildung darzustellen. Der entscheidende Unterschied zu unseren bisherigen Plots ist, dass wir nun die Zeichenfläche mit
fig, axes = plt.subplots(1, 2, figsize=(15, 10))
erzeugen und die objektorientierte Schnittstelle benutzen. Die obige
Code-Zeile erstellt eine Abbildung (fig) mit 1 Zeile und 2 Spalten von Plots.
Das axes-Array enthält die beiden einzelnen Plot-Bereiche. Auf die einzelnen
Plots können wir folgendermaßen zugreifen:
axes[0]: der erste Plot (links)axes[1]: der zweite Plot (rechts)
Anstelle der gewohnten Funktion plt.bar() verwenden wir nun
axes[0].bar(...)oder axes[1].bar(...). Auch werden die Funktionen wir
plt.title()zu Methoden, die sich auf das konkrete Objekt beziehen, wie
axes[0].set_title(). Wir verwenden noch weitere Optionen zum Styling der
Plots.
# Daten für Eintracht Frankfurt
eintracht_frankfurt = data[data['Club'] == 'Eintracht Frankfurt']
# 1x2 Subplot-Layout erstellen
fig, axes = plt.subplots(1, 2, figsize=(15, 10))
# Plot 1: Alter
axes[0].bar(eintracht_frankfurt.index, eintracht_frankfurt['Age'],
color='skyblue', alpha=0.7)
axes[0].set_title('Alter der Spieler')
axes[0].set_ylabel('Alter')
# Erst die Tick-Positionen setzen, dann die Labels
axes[0].set_xticks(range(len(eintracht_frankfurt)))
axes[0].set_xticklabels(eintracht_frankfurt.index, rotation=45, ha='right', fontsize=8)
# Plot 2: Spielminuten
axes[1].bar(eintracht_frankfurt.index, eintracht_frankfurt['Mins'],
color='lightgreen', alpha=0.7)
axes[1].set_title('Spielminuten')
axes[1].set_ylabel('Minuten')
axes[1].set_xticks(range(len(eintracht_frankfurt)))
axes[1].set_xticklabels(eintracht_frankfurt.index, rotation=45, ha='right', fontsize=8)
plt.suptitle('Spielerstatistiken Eintracht Frankfurt 20/21', fontsize=16)
plt.tight_layout()
plt.show()
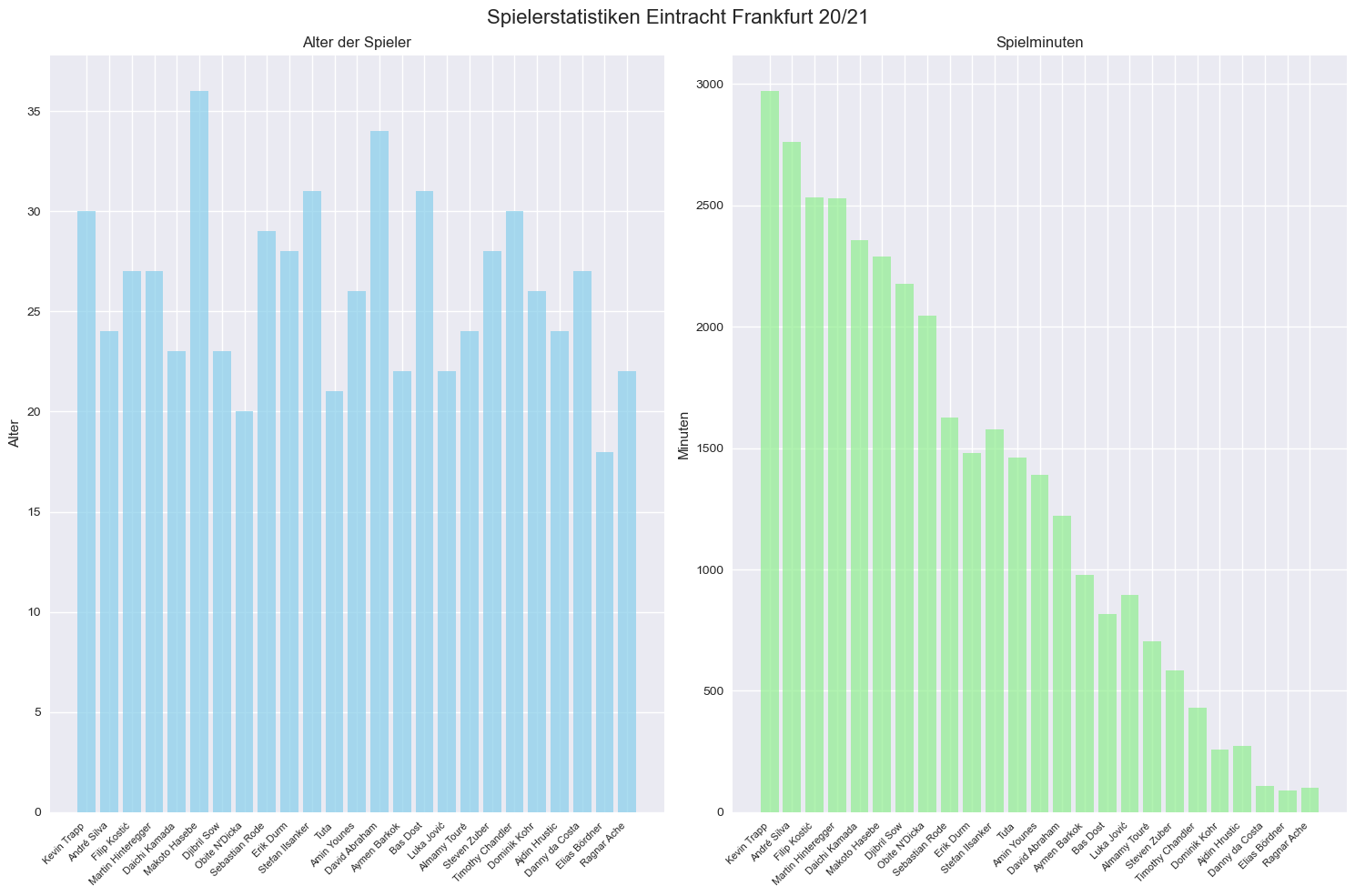
Korrelationsanalyse mit Streudiagrammen#
Hier sehen wir eine wichtige statistische Methode: Korrelationsanalysen untersuchen, ob und wie stark zwei Variablen miteinander zusammenhängen. In unserem Beispiel fragen wir uns: Gibt es einen Zusammenhang zwischen Spielminuten und Toren? Oder zwischen Alter und Einsatzzeit?
ig, axes = plt.subplots(2, 2, figsize=(12, 8))
# Streudiagramm: Spielminuten vs. Tore
axes[0, 0].scatter(data['Mins'], data['Goals'], alpha=0.6, color='red')
axes[0, 0].set_xlabel('Spielminuten')
axes[0, 0].set_ylabel('Tore')
axes[0, 0].set_title('Spielminuten vs. Tore')
# Streudiagramm: Alter vs. Spielminuten
axes[0, 1].scatter(data['Age'], data['Mins'], alpha=0.6, color='blue')
axes[0, 1].set_xlabel('Alter')
axes[0, 1].set_ylabel('Spielminuten')
axes[0, 1].set_title('Alter vs. Spielminuten')
# Streudiagramm: Tore vs. Torvorbereitungen (= Assists)
axes[1, 0].scatter(data['Goals'], data['Assists'], alpha=0.6, color='green')
axes[1, 0].set_xlabel('Tore')
axes[1, 0].set_ylabel('Assists')
axes[1, 0].set_title('Tore vs. Assists')
# Streudiagramm: Spielminuten vs. Torvorbereitungen (= Assists)
axes[1, 1].scatter(data['Mins'], data['Assists'], alpha=0.6, color='orange')
axes[1, 1].set_xlabel('Spielminuten')
axes[1, 1].set_ylabel('Assists')
axes[1, 1].set_title('Spielminuten vs. Assists')
plt.suptitle('Korrelationsanalyse Bundesliga-Spieler', fontsize=16)
plt.tight_layout()
plt.show()
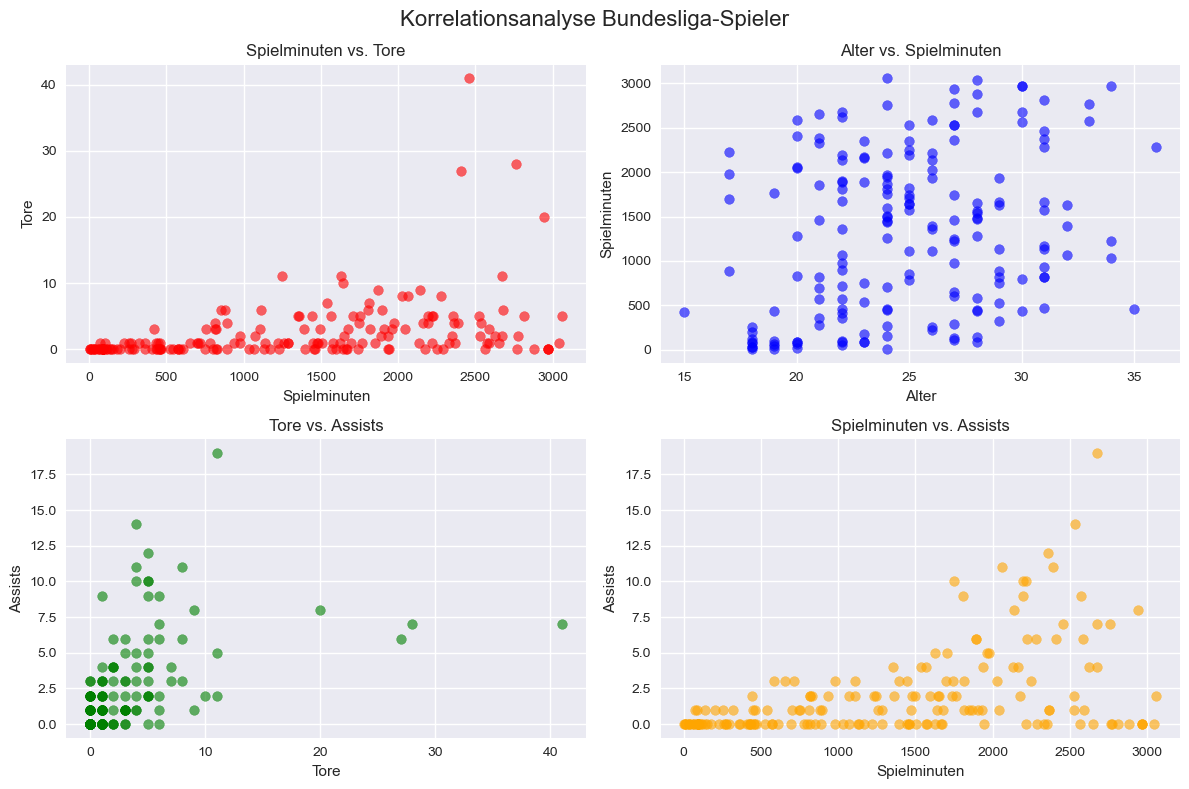
Hier sehen wir die wichtigsten Muster in Streudiagrammen:
Positive Korrelation: Die Punkte bilden eine aufsteigende Linie: je höher die Ursache, desto höher die Wirkung. Beim Beispiel Spielminuten vs. Tore können wir interpretieren: “Wer mehr spielt, erzielt tendenziell mehr Tore”.
Negative Korrelation: Die Punkte bilden eine absteigende Linie: je höher die Ursache, desto niedriger die Wirkung. Beim Beispiel Alter vs. Spielminuten können wir interpretieren: “Ältere Spieler bekommen tendenziell weniger Einsatzzeit”.
Keine Korrelation: Die Punkte sind zufällig verteilt: kein erkennbares Muster. Wir interpretieren: “Zwischen den Variablen gibt es keinen systematischen Zusammenhang”.
Export von Grafiken#
Für die Verwendung in Dokumenten oder Präsentationen müssen Grafiken exportiert werden:
# Beispiel-Plot erstellen
plt.figure(figsize=(10, 6))
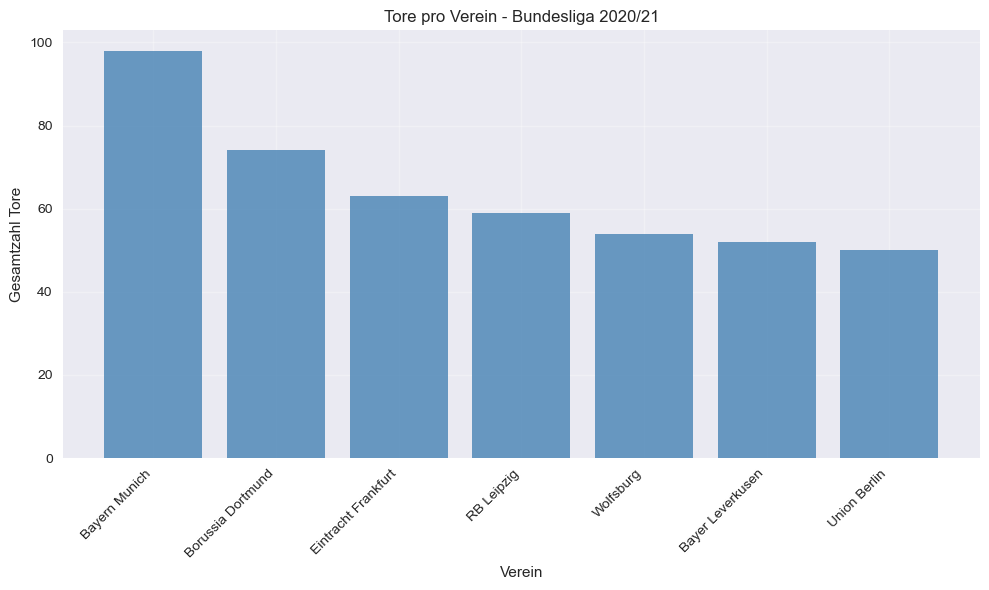
verein_tore = data.groupby('Club')['Goals'].sum().sort_values(ascending=False)
plt.bar(verein_tore.index, verein_tore.values, color='steelblue', alpha=0.8)
plt.xlabel('Verein')
plt.ylabel('Gesamtzahl Tore')
plt.title('Tore pro Verein - Bundesliga 2020/21')
plt.xticks(rotation=45, ha='right')
plt.grid(True, alpha=0.3)
plt.tight_layout()
# Export in verschiedenen Formaten
plt.savefig('bundesliga_tore.png', dpi=300, bbox_inches='tight') # Für Web/Präsentationen
plt.savefig('bundesliga_tore.pdf', bbox_inches='tight') # Für LaTeX/Publikationen
plt.savefig('bundesliga_tore.svg', bbox_inches='tight') # Für Vektorgrafiken
plt.show()
Zusammenfassung und Ausblick#
In diesem Kapitel haben wir gelernt, wie man DataFrames professionell visualisiert. Diese Techniken bilden die Grundlage für die Datenvisualisierung in der Praxis. Mit DataFrames und Matplotlib können wir reale Datensätze ansprechend präsentieren. Mit der Korrelationsanalyse haben wir auch einen ersten Schritt Richtung Data Science gemacht. Wie wir Trends und Muster in Daten finden, werden wir im nächsten Kapitel lernen, wenn wir uns der Regression widmen.

