12.2 Diskrete Daten und Häufigkeiten#
Lernziele#
Lernziele
Sie können diskrete Daten als Balkendiagramm visualisieren.
Sie können kontinuierliche Daten als Histogramm darstellen.
Sie verstehen den Unterschied zwischen Balkendiagrammen und Histogrammen.
Sie können die Anzahl der Bins bei Histogrammen anpassen.
Sie können Balken- und Histogramme mit Farben gestalten.
Balkendiagramme#
Ein Balkendiagramm wird mit der Funktion bar() erstellt. Balkendiagramme
eignen sich zur Darstellung von diskreten, kategorialen Daten. Angenommen, wir
möchten auswerten, wie viele Nutzer/innen in campUAS auf die Jupyter Notebooks
zum Download zugegriffen haben:
Woche |
Anzahl Nutzer/innen |
|---|---|
2 |
14 |
3 |
12 |
4 |
10 |
5 |
10 |
6 |
9 |
Dann wird das Balkendiagramm mit folgendem Code erzeugt:
import matplotlib.pyplot as plt
# Daten
x = [2, 3, 4, 5, 6]
y = [14, 12, 10, 10, 9]
# Balkendiagramm
plt.figure()
plt.bar(x, y)
plt.xlabel('Woche')
plt.ylabel('Anzahl Nutzer/innen')
plt.title('Zugriff auf Jupyter Notebooks zum Download WiSe 2021/22')
plt.show()
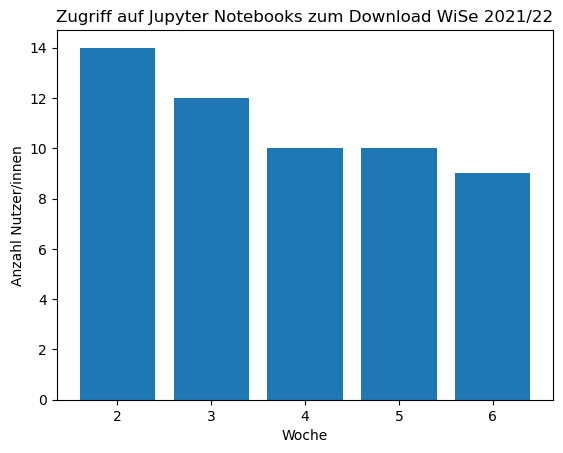
Farben können mit dem optionalen Argument color= eingestellt werden. Dabei
funktionieren häufig einfach die englischen Bezeichnungen für grundlegende
Farben wie beispielsweise red, green, blue. Eine Alternative dazu ist, den
RGB-Wert zu spezifizieren, also den Rot-Anteil, den Grün-Anteil und den
Blau-Anteil. Details finden Sie in der Matplotlib-Dokumentation:
Im folgenden Balkendiagramm sind die Balken grau dargestellt.
# Daten
x = [2, 3, 4, 5, 6]
y = [14, 12, 10, 10, 9]
# Balkendiagramm mit Farbe
plt.figure()
plt.bar(x, y, color='gray')
plt.xlabel('Woche')
plt.ylabel('Anzahl Nutzer/innen')
plt.title('Zugriff auf Jupyter Notebooks zum Download WiSe 2021/22')
plt.show()
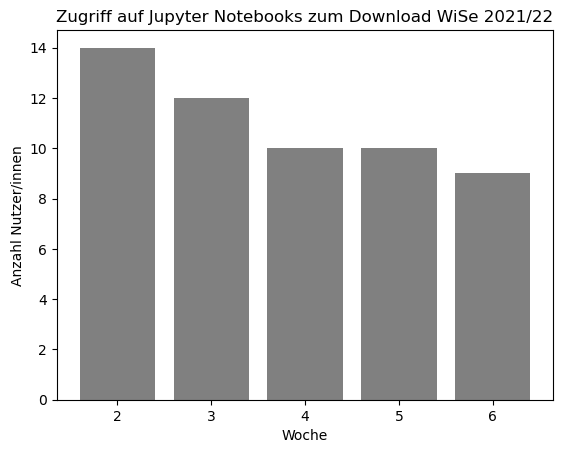
Balkendiagramme eignen sich besonders gut für den Vergleich von Kategorien. Hier
ein weiteres Beispiel mit verschiedenen Programmiersprachen und ihrer
Beliebtheit. Bei diesem Beispiel färben wir auch noch die Balken ein. Dazu
übergeben wir dem Argument color eine Liste mit Strings, die die Farben
Hex-Code spezifiziert. Mehr Details zu Hex-Codes für Farben finden Sie hier:
https://www.color-hex.com.
# Daten (fiktive Umfrage)
sprachen = ['Python', 'Java', 'C++', 'JavaScript', 'C#']
beliebtheit = [85, 78, 65, 82, 58]
# Balkendiagramm
plt.figure()
plt.bar(sprachen, beliebtheit, color=['#3776ab', '#f89820', '#00599c', '#f7df1e', '#239120'])
plt.xlabel('Programmiersprache')
plt.ylabel('Beliebtheit (%)')
plt.title('Beliebtheit von Programmiersprachen unter Studierenden')
plt.show()
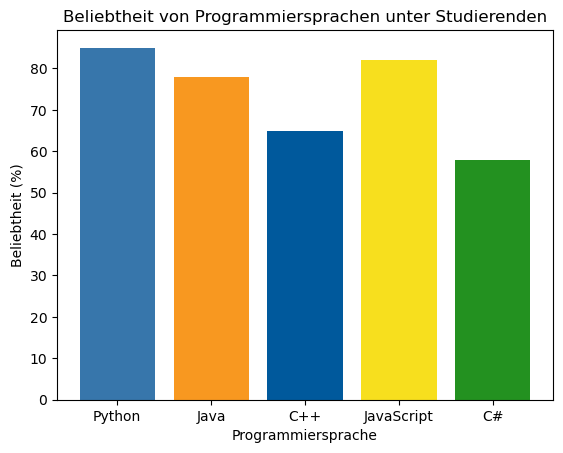
Mini-Übung
Hier ist eine Tabelle mit den Zugriffszahlen auf die Jupyter Notebooks in der Vorlesung Angewandte Informatik. Bitte stellen Sie die Daten als Balkendiagramm inklusive Beschriftungen dar. Färben Sie die Balken schwarz.
Woche |
Anzahl Nutzer/innen |
|---|---|
3 |
9 |
4 |
17 |
5 |
15 |
6 |
10 |
7 |
11 |
# Hier Ihr Code:
Lösung
import matplotlib.pyplot as plt
x = [3, 4, 5, 6, 7]
y = [9, 17, 15, 10, 11]
plt.figure()
plt.bar(x, y, color='black')
plt.xlabel('Woche')
plt.ylabel('Anzahl Nutzer/innen')
plt.title('Zugriffszahlen Jupyter Notebooks - Angewandte Informatik')
plt.show()
Histogramme#
Während Balkendiagramme für diskrete, kategoriale Daten verwendet werden, dienen Histogramme zur Darstellung der Verteilung kontinuierlicher Daten. Ein Histogramm zeigt, wie häufig bestimmte Wertebereiche in einem Datensatz vorkommen.
Der wichtigste Unterschied: Bei Balkendiagrammen sind die Kategorien fest vorgegeben (z.B. Wochentage, Programmiersprachen), bei Histogrammen werden die kontinuierlichen Daten in Intervalle (sogenannte “Bins”) unterteilt.
Erstellen wir zunächst einen Datensatz mit kontinuierlichen Daten:
import numpy as np
import matplotlib.pyplot as plt
# Simuliere Körpergrößen von 1000 Personen (normalverteilt)
np.random.seed(42) # Für reproduzierbare Ergebnisse
koerpergroessen = np.random.normal(175, 8, 1000) # Mittelwert 175cm, Standardabweichung 8cm
# Histogramm erstellen
plt.figure()
plt.hist(koerpergroessen, bins=30)
plt.xlabel('Körpergröße [cm]')
plt.ylabel('Häufigkeit')
plt.title('Verteilung der Körpergrößen')
plt.show()
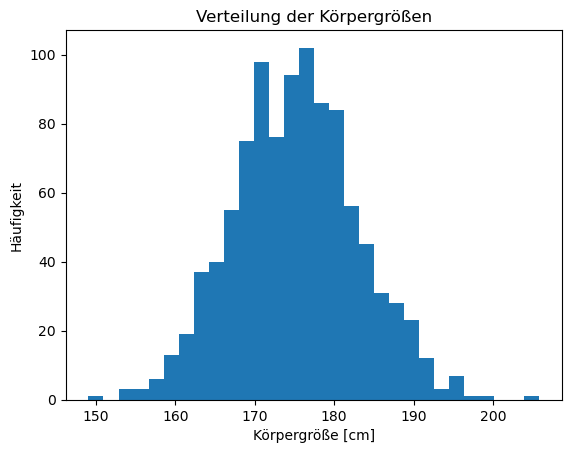
Die Funktion hist() nimmt die Rohdaten und erstellt automatisch ein
Histogramm. Der Parameter bins bestimmt, in wie viele Intervalle die Daten
aufgeteilt werden. Mehr Bins führen zu einer feineren Aufteilung, weniger Bins
zu einer gröberen.
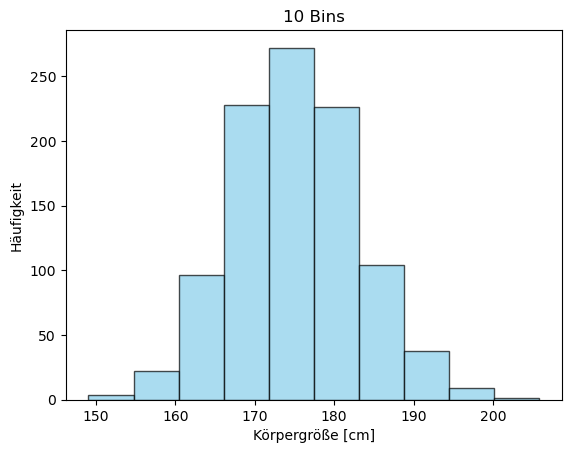
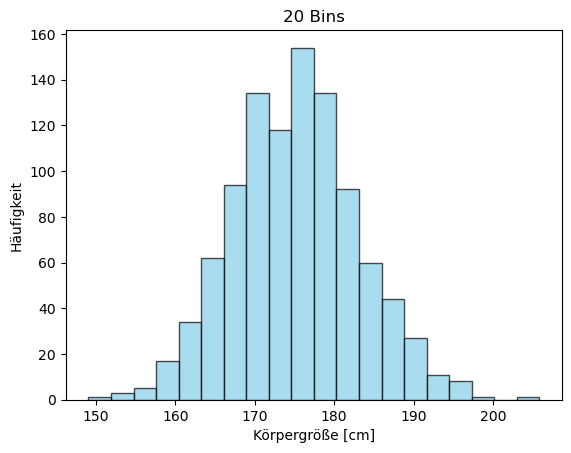
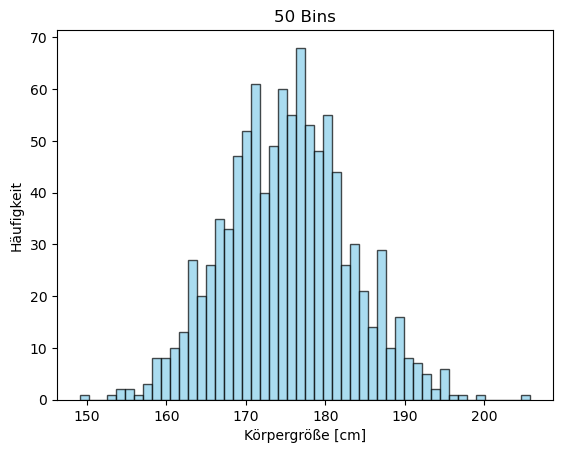
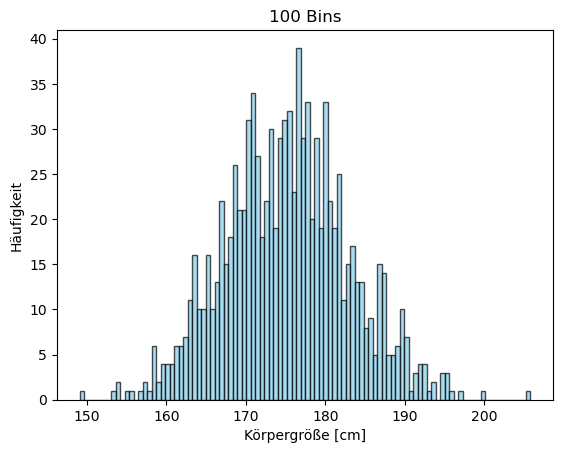
Schauen wir uns den Effekt verschiedener Bin-Anzahlen an. Zusätzlich nutzen wir
noch die Optionen alpha (Transparenzgrad), color (Farbe) und edgecolor
(Farbe des Rahmens um die Balken), um die Bins besser zu visualisieren.
# Verschiedene Bin-Anzahlen vergleichen
anzahl_bins = [10, 20, 50, 100]
titel = ['10 Bins', '20 Bins', '50 Bins', '100 Bins']
for i in range(4):
plt.figure()
plt.hist(koerpergroessen, bins=anzahl_bins[i], alpha=0.7, color='skyblue', edgecolor='black')
plt.xlabel('Körpergröße [cm]')
plt.ylabel('Häufigkeit')
plt.title(titel[i])
Mini-Übung
Erstellen Sie ein Histogramm für simulierte Reaktionszeiten:
Generieren Sie 500 Zufallszahlen mit Mittelwert 0.25 und Standardabweichung 0.05
Verwenden Sie 25 Bins
Färben Sie das Histogramm orange
Beschriften Sie die Achsen: x-Achse “Reaktionszeit [s]”, y-Achse “Häufigkeit”
Titel: “Verteilung der Reaktionszeiten”
# Hier Ihr Code
Lösung
import numpy as np
import matplotlib.pyplot as plt
# Daten generieren
np.random.seed(42)
reaktionszeiten = np.random.normal(0.25, 0.05, 500)
# Histogramm erstellen
plt.figure()
plt.hist(reaktionszeiten, bins=25, color='orange', alpha=0.7, edgecolor='black')
plt.xlabel('Reaktionszeit [s]')
plt.ylabel('Häufigkeit')
plt.title('Verteilung der Reaktionszeiten')
plt.grid(True, alpha=0.3)
plt.show()
Was ist der Unterschied zwischen Balkendiagramm und Histogramm?#
Um den Unterschied zwischen Balkendiagramm und Histogramm zu verdeutlichen, schauen wir uns Daten von Autos als Beispiel an.
Mit dem Balkendiagramm visualisieren wir diskrete Daten wie beispielsweise die Anzahl der verkauften Autos pro Marke.
# Anzahl verkaufter Autos pro Marke (diskrete Kategorien)
marken = ['BMW', 'Mercedes', 'Audi', 'VW', 'Ford']
verkaufte_autos = [45, 38, 52, 67, 23]
plt.figure()
plt.bar(marken, verkaufte_autos)
plt.xlabel('Automarke')
plt.ylabel('Anzahl verkaufter Autos')
plt.title('Balkendiagramm: Diskrete Kategorien')
plt.show();
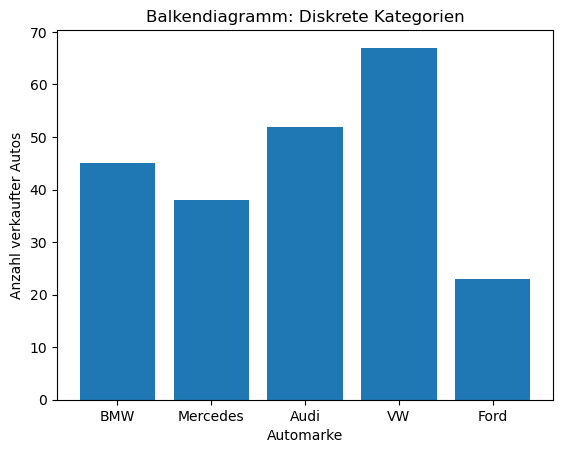
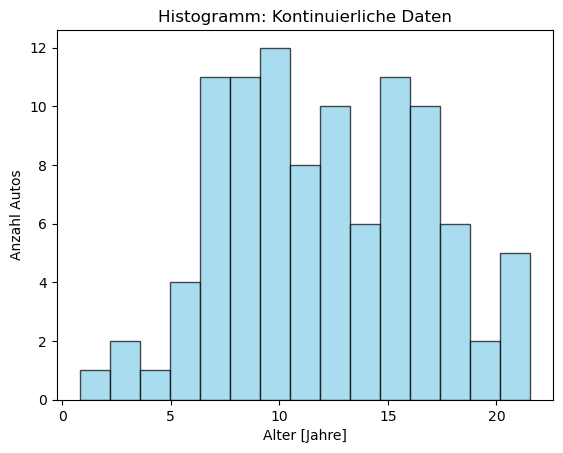
Wenn es aber nun darum geht, darzustellen, wie viele Autos ein bestimmtes Alter in Jahren haben, ist ein Balkendiagramm unübersichtlich. Besser ist es, die Jahre zuerst zu clustern.
# Alter der Autos (kontinuierliche Daten)
np.random.seed(123)
alter = np.random.normal(12, 4, 100)
plt.figure()
plt.hist(alter, bins=15, alpha=0.7, color='skyblue', edgecolor='black')
plt.xlabel('Alter [Jahre]')
plt.ylabel('Anzahl Autos')
plt.title('Histogramm: Kontinuierliche Daten')
plt.show();
Zusammenfassung und Ausblick#
In diesem Kapitel haben wir zwei wichtige Visualisierungstypen für verschiedene Datenarten kennengelernt. Balkendiagramme eignen sich für diskrete, kategoriale Daten und ermöglichen den direkten Vergleich zwischen verschiedenen Kategorien. Histogramme zeigen die Verteilung kontinuierlicher Daten und helfen dabei, Muster und Häufigkeiten in großen Datensätzen zu erkennen. Im nächsten Kapitel werden wir lernen, wie wir diese Techniken auf reale Datensätze anwenden können.

