11.2 Arbeiten mit Tabellendaten#
Eine Tabellenkalkulationssoftware wie LibreOffice Calc, Excel oder Number ist nicht nur nützlich, um Daten zu sammeln, sondern auch um sie zu bearbeiten. In diesem Kapitel geht es darum zu lernen, wie mit Pandas auf einzelne Zeilen, Spalten oder Zellen zugegriffen wird.
Lernziele#
Lernziele
Sie können auf ganze Zeilen und Spalten zugreifen:
Zugriff auf eine einzelne Zeile oder Spalte, indem ein Index spezifiziert wird
Zugriff auf mehrere zusammenhängende Zeilen oder Spalten (Slice)
Zugriff auf mehrere unzusammenhängende Zeilen oder Spalten (Selektion)
Sie können auf einzelne oder mehrere Zellen der Tabelle zugreifen.
Sie können ein DataFrame-Objekt nach einer Eigenschaft filtern.
Zugriff auf Spalten#
Für die folgenden Demonstrationen wollen wir wiederum die Spielerdaten der Top7-Fußballvereine der Bundesligasaison 2020/21 verwenden. Importieren Sie bitte vorab die Daten und verwenden Sie die 1. Spalte (= Namen) als Zeilenindex.
import pandas as pd
data = pd.read_csv('bundesliga_top7_offensive.csv', index_col=0)
data.head(10)
| Club | Nationality | Position | Age | Matches | Starts | Mins | Goals | Assists | Penalty_Goals | Penalty_Attempted | xG | xA | Yellow_Cards | Red_Cards | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Name | |||||||||||||||
| Manuel Neuer | Bayern Munich | GER | GK | 34 | 33 | 33 | 2970 | 0 | 0 | 0 | 0 | 0.00 | 0.01 | 1 | 0 |
| Thomas Müller | Bayern Munich | GER | MF | 30 | 32 | 31 | 2674 | 11 | 19 | 1 | 1 | 0.24 | 0.39 | 0 | 0 |
| David Alaba | Bayern Munich | AUT | DF,MF | 28 | 32 | 30 | 2675 | 2 | 4 | 0 | 0 | 0.04 | 0.08 | 4 | 0 |
| Jérôme Boateng | Bayern Munich | GER | DF | 31 | 29 | 29 | 2368 | 1 | 1 | 0 | 0 | 0.01 | 0.02 | 6 | 0 |
| Robert Lewandowski | Bayern Munich | POL | FW | 31 | 29 | 28 | 2458 | 41 | 7 | 8 | 9 | 1.16 | 0.13 | 4 | 0 |
| Joshua Kimmich | Bayern Munich | GER | MF | 25 | 27 | 25 | 2194 | 4 | 10 | 0 | 0 | 0.10 | 0.27 | 4 | 0 |
| Kingsley Coman | Bayern Munich | FRA | FW,MF | 24 | 29 | 23 | 1752 | 5 | 10 | 0 | 0 | 0.21 | 0.34 | 1 | 0 |
| Benjamin Pavard | Bayern Munich | FRA | DF | 24 | 24 | 22 | 1943 | 0 | 0 | 0 | 0 | 0.02 | 0.09 | 3 | 0 |
| Alphonso Davies | Bayern Munich | CAN | DF | 19 | 23 | 22 | 1763 | 1 | 2 | 0 | 0 | 0.01 | 0.04 | 2 | 1 |
| Serge Gnabry | Bayern Munich | GER | FW,MF | 25 | 27 | 20 | 1644 | 10 | 2 | 0 | 0 | 0.44 | 0.25 | 4 | 0 |
Einzelne Spalte#
Der Zugriff auf Spalten wird am häufigsten gebraucht, da üblicherweise in den
Spalten die Merkmale der Datenobjekte stehen. Daher bietet Pandas dafür einen
direkten Zugriff über die eckigen Klammern [ ] an.
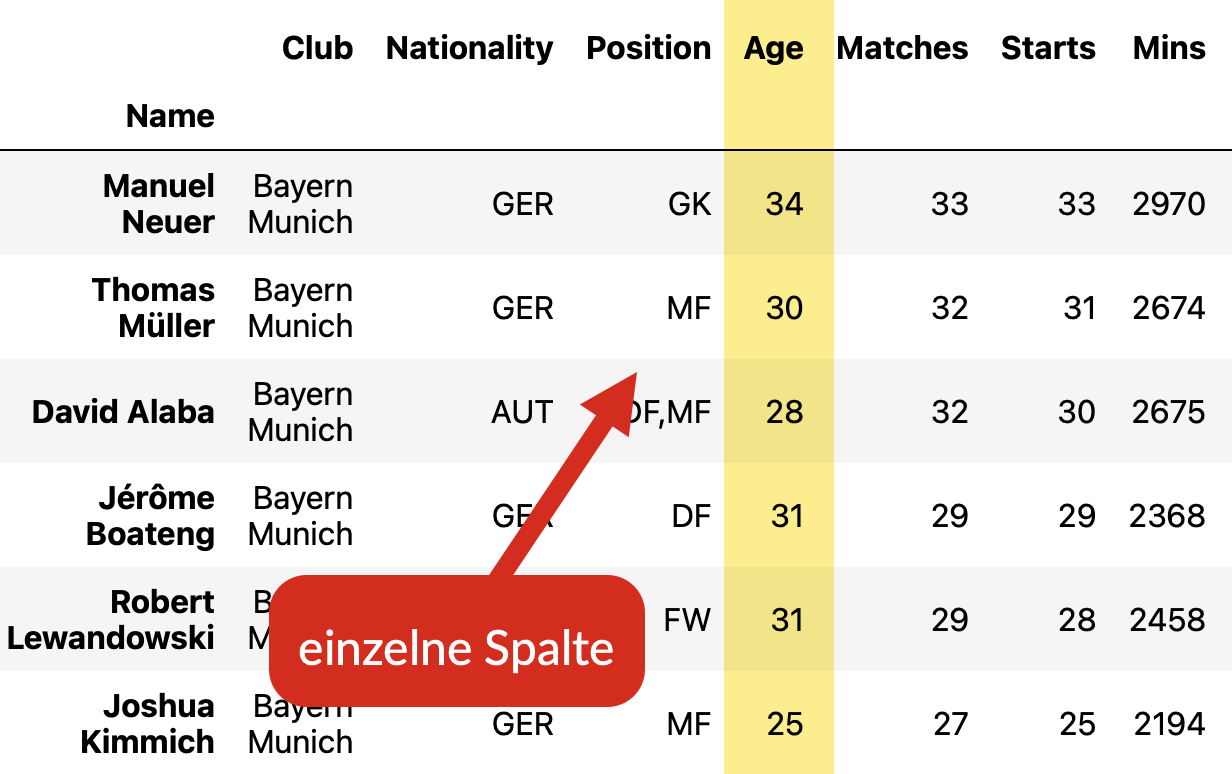
Fig. 9 Auf eine einzelne Spalte der Tabelle wird mit [spaltenindex] zugegriffen.#
Das Alter der Fußballspieler erhalten wir somit mit dem Spaltenindex Age.
alter = data['Age']
print(alter)
Name
Manuel Neuer 34
Thomas Müller 30
David Alaba 28
Jérôme Boateng 31
Robert Lewandowski 31
..
Loris Karius 27
Akaki Gogia 28
Leon Dajaku 19
Tim Maciejewski 19
Joshua Mees 24
Name: Age, Length: 177, dtype: int64
Selektion Spalten per Liste#
Wir möchten nun die Anzahl der Spiele (Matches) und die Anzahl der gespielten
Minuten in der kompletten Saison (Mins) auswerten, um beispielsweise die
durchschnittliche Minutenzahl pro Spiel zu ermitteln. Da die Spalten nicht
nebeneinander liegen, müssen wir eine Liste benutzen, um sie zu selektieren. Die
Auswahl der Spalten wird in der Fachsprache Selektion genannt.

Fig. 10 Auf mehrere unzusammenhängende Spalten der Tabelle wird mit [list]
zugegriffen. Das nennt man Selektion.#
Das folgende Code-Beispiel demonstriert die Selektion zweier Spalten.
spiele_minuten = data[['Matches', 'Mins']]
print(spiele_minuten)
Matches Mins
Name
Manuel Neuer 33 2970
Thomas Müller 32 2674
David Alaba 32 2675
Jérôme Boateng 29 2368
Robert Lewandowski 29 2458
... ... ...
Loris Karius 4 292
Akaki Gogia 7 140
Leon Dajaku 2 37
Tim Maciejewski 1 8
Joshua Mees 1 5
[177 rows x 2 columns]
Mini-Übung
Lassen Sie sich die folgenden Spalten anzeigen:
Nationality
Nationality, Age und Matches
# Hier Ihr Code
Lösung
data_spalte = data['Nationality']
data_selektion = data[['Nationality','Age', 'Matches']]
print(data_spalte)
print(data_selektion)
Zugriff auf Zeilen#
Der Zugriff auf Zeilen erfordert eine Erweiterung der Syntax. Über das Attribut
loc[] stellt Pandas nicht nur den Zugriff auf Zeilen zur Verfügung, sondern
ermöglicht auch fortgeschritte Zugriffsmöglichkeiten wie beispielsweise das
Slicing, wie wir später sehen werden. Aber zunächst starten wir mit dem Zugriff
auf einzelne Zeilen.
Einzelne Zeile#
Uns interessieren die Spielerdaten von Thomas Müller näher.
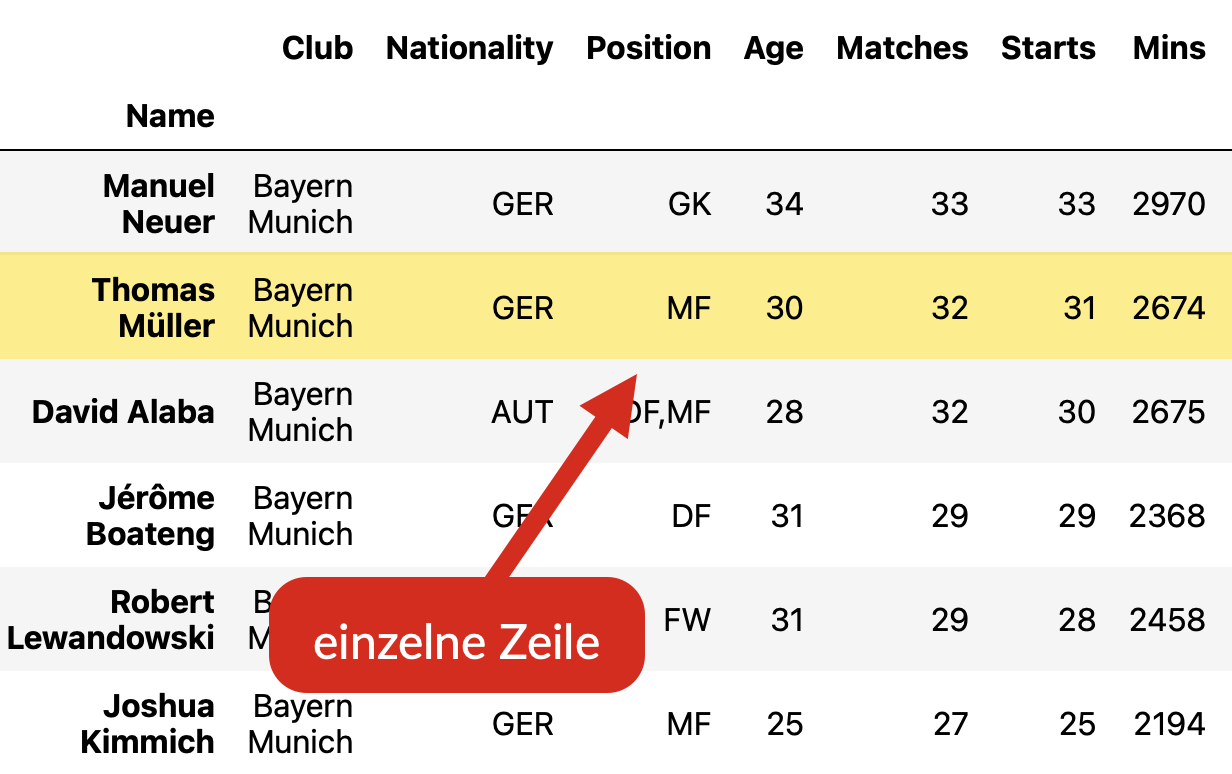
Fig. 11 Auf eine einzelne Zeile der Tabelle wird mit .loc[zeilenindex] zugegriffen.#
Um eine ganze Zeile aus der Tabelle herauszugreifen, verwenden wir das Attribut
.loc[zeilenindex] und geben in eckigen Klammern den Index der Zeile an, die
wir betrachten wollen. Da wir beim Import die Namen als Zeileindex gesetzt
haben, lautet der Zugriff also wie folgt:
zeile = data.loc['Thomas Müller']
print(zeile)
Club Bayern Munich
Nationality GER
Position MF
Age 30
Matches 32
Starts 31
Mins 2674
Goals 11
Assists 19
Penalty_Goals 1
Penalty_Attempted 1
xG 0.24
xA 0.39
Yellow_Cards 0
Red_Cards 0
Name: Thomas Müller, dtype: object
Selektion Zeilen per Liste#
Wenn wir auf mehrere Zeilen zugreifen wollen, die nicht zusammenhängen, so nennt man das wie bei den Spalten ebenfalls Selektion.
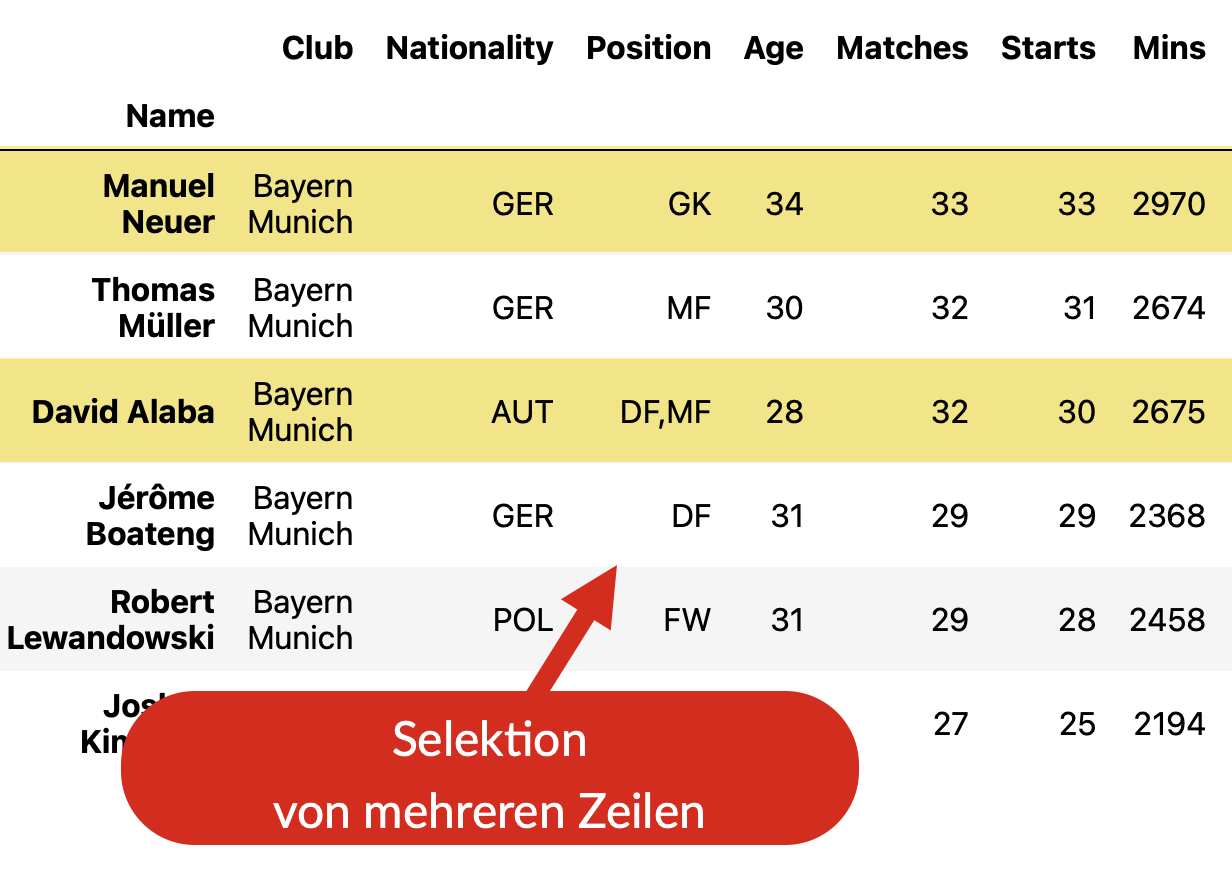
Fig. 12 Auf mehrere unzusammenhängende Zeilen der Tabelle wird mit .loc[list]
zugegriffen. Das nennt man Selektion.#
Um mehrere unzusammenhängende Zeilen zu selektieren, übergeben wir .loc[] eine
Liste mit den gewünschten Zeilenindizes.
zeilen_selektion = data.loc[['Manuel Neuer', 'David Alaba']]
print(zeilen_selektion)
Club Nationality Position Age Matches Starts Mins \
Name
Manuel Neuer Bayern Munich GER GK 34 33 33 2970
David Alaba Bayern Munich AUT DF,MF 28 32 30 2675
Goals Assists Penalty_Goals Penalty_Attempted xG xA \
Name
Manuel Neuer 0 0 0 0 0.00 0.01
David Alaba 2 4 0 0 0.04 0.08
Yellow_Cards Red_Cards
Name
Manuel Neuer 1 0
David Alaba 4 0
Mini-Übung
Lassen Sie sich die folgenden Zeilen anzeigen:
Kingsley Coman
Kingsley Coman bis Alphonso Davies
Robert Lewandowski, Kingsley Coman und Serge Gnabry
# Hier Ihr Code
Lösung
data_zeile = data.loc['Kingsley Coman']
data_selektion = data.loc[['Robert Lewandowski','Kingsley Coman', 'Serge Gnabry']]
print(data_zeile)
print(data_selektion)
Slicing#
Wenn wir auf mehrere Zeilen oder Spalten gleichzeitig zugreifen wollen, gibt es zwei Möglichkeiten:
Zwischen den einzelnen Zeilen/Spalten sind Lücken, wir haben eine unzusammenhängende Selektion.
Die Zeilen oder Spalten folgen direkt aufeinander, sind also zusammenhängend.
Den ersten Fall haben wir bereits oben dargestellt. Bei Spalten wird die
Selektion über eine Liste und eckige Klammern [] realisiert, bei Zeilen über
eine Liste, die in .loc[] eingesetzt wird.
Der Zugriff auf zusammenhängende Bereiche wird in der Informatik Slicing genannt. Wir werden uns die beiden Fälle
Slicing für Zeilen
Slicing für Spalten
anschauen, aber zunächst betrachten wir das Slicing von Zeilen.
Slicing von Zeilen#
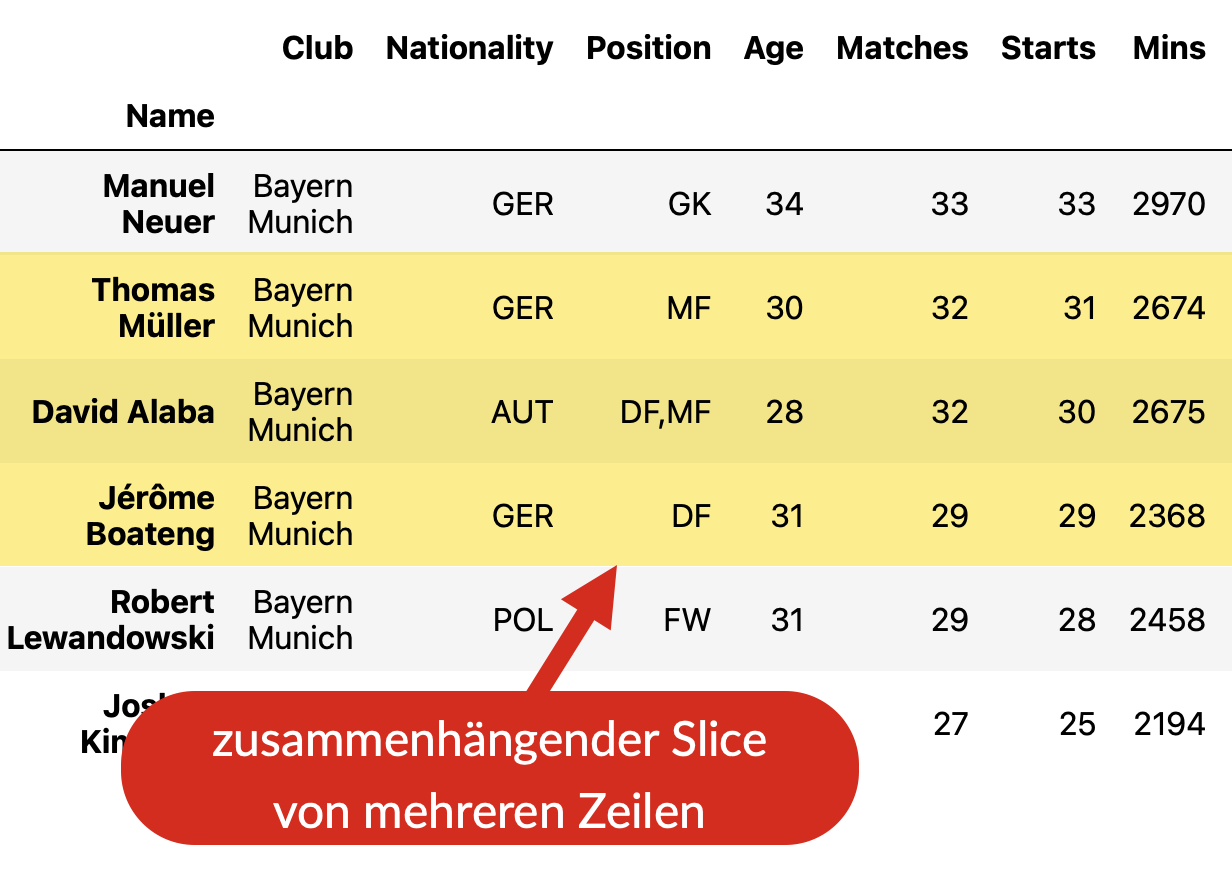
Fig. 13 Auf mehrere zusammenhängende Zeilen der Tabelle wird mit .loc[start:stopp]
zugegriffen. Das nennt man Slicing.#
Bei der Angabe des Bereiches gibt man den Anfangsindex gefolgt von einem Doppelpunkt an und dann den Endindex der letzten Zeile, die “herausgeschnitten” werden soll.
zeilen_slice = data.loc['Thomas Müller' : 'Jérôme Boateng']
print(zeilen_slice)
Club Nationality Position Age Matches Starts \
Name
Thomas Müller Bayern Munich GER MF 30 32 31
David Alaba Bayern Munich AUT DF,MF 28 32 30
Jérôme Boateng Bayern Munich GER DF 31 29 29
Mins Goals Assists Penalty_Goals Penalty_Attempted xG \
Name
Thomas Müller 2674 11 19 1 1 0.24
David Alaba 2675 2 4 0 0 0.04
Jérôme Boateng 2368 1 1 0 0 0.01
xA Yellow_Cards Red_Cards
Name
Thomas Müller 0.39 0 0
David Alaba 0.08 4 0
Jérôme Boateng 0.02 6 0
Beim Slicing können wir den Angangsindex oder den Endindex oder sogar beides weglassen. Wenn wir den Anfangsindex weglassen, fängt Pandas bei der ersten Zeile an. Lassen wir den Endindex weg, geht der Slice automatisch bis zum Ende.
Im folgenden Beispiel startet der Slice bei ‘Robert Lewandowski’und geht bis zur letzten Zeile. Obwohl nicht alle Zeilendargestellt werden, erkennen wir das an der Anzahl der Zeilen: 173 rows (und 15 Spalten columns). Zur Erinnerung, es sind insgesamt 177 Zeilen.
data_slice_from_lewandowski = data.loc['Robert Lewandowski': ]
print(data_slice_from_lewandowski)
Club Nationality Position Age Matches Starts \
Name
Robert Lewandowski Bayern Munich POL FW 31 29 28
Joshua Kimmich Bayern Munich GER MF 25 27 25
Kingsley Coman Bayern Munich FRA FW,MF 24 29 23
Benjamin Pavard Bayern Munich FRA DF 24 24 22
Alphonso Davies Bayern Munich CAN DF 19 23 22
... ... ... ... ... ... ...
Loris Karius Union Berlin GER GK 27 4 3
Akaki Gogia Union Berlin GER FW 28 7 0
Leon Dajaku Union Berlin GER FW 19 2 0
Tim Maciejewski Union Berlin GER MF 19 1 0
Joshua Mees Union Berlin GER FW 24 1 0
Mins Goals Assists Penalty_Goals Penalty_Attempted \
Name
Robert Lewandowski 2458 41 7 8 9
Joshua Kimmich 2194 4 10 0 0
Kingsley Coman 1752 5 10 0 0
Benjamin Pavard 1943 0 0 0 0
Alphonso Davies 1763 1 2 0 0
... ... ... ... ... ...
Loris Karius 292 0 0 0 0
Akaki Gogia 140 0 1 0 0
Leon Dajaku 37 0 0 0 0
Tim Maciejewski 8 0 0 0 0
Joshua Mees 5 0 0 0 0
xG xA Yellow_Cards Red_Cards
Name
Robert Lewandowski 1.16 0.13 4 0
Joshua Kimmich 0.10 0.27 4 0
Kingsley Coman 0.21 0.34 1 0
Benjamin Pavard 0.02 0.09 3 0
Alphonso Davies 0.01 0.04 2 1
... ... ... ... ...
Loris Karius 0.00 0.00 0 0
Akaki Gogia 0.09 0.28 1 0
Leon Dajaku 0.00 0.00 0 0
Tim Maciejewski 0.00 0.00 0 0
Joshua Mees 2.02 0.00 0 0
[173 rows x 15 columns]
Slicing von Spalten#
Wenden wir uns nun dem Slicing von Spalten zu. Möchten wir beispielsweise die
Anzahl der Spiele (Matches), die ein Spieler in der Saison absolviert hat, mit
der Anzahl der Spiele, in denen er vom Anfang an auf dem Platz stand (Starts)
vergleichen, so können wir die beiden aufeinanderfolgenden Spalten ‘Matches’ und
‘Starts’ als sogenannten Slice ausschneiden. Dazu müssen wir jedoch das
Attribut .loc[] verwenden, das uns fortgeschrittene Techniken des Zugriffs
bietet. Allerdings müssen wir Python mitteilen, dass diesmal Spalten und nicht
Zeilen gemeint sind. Die Dokumentation von loc[] zeigt uns, dass Spalten nach
einem Komma angegeben werden. Damit alle Zeilen dabei sind, brauchen wir als
erstes Argument den Doppelpunkt.
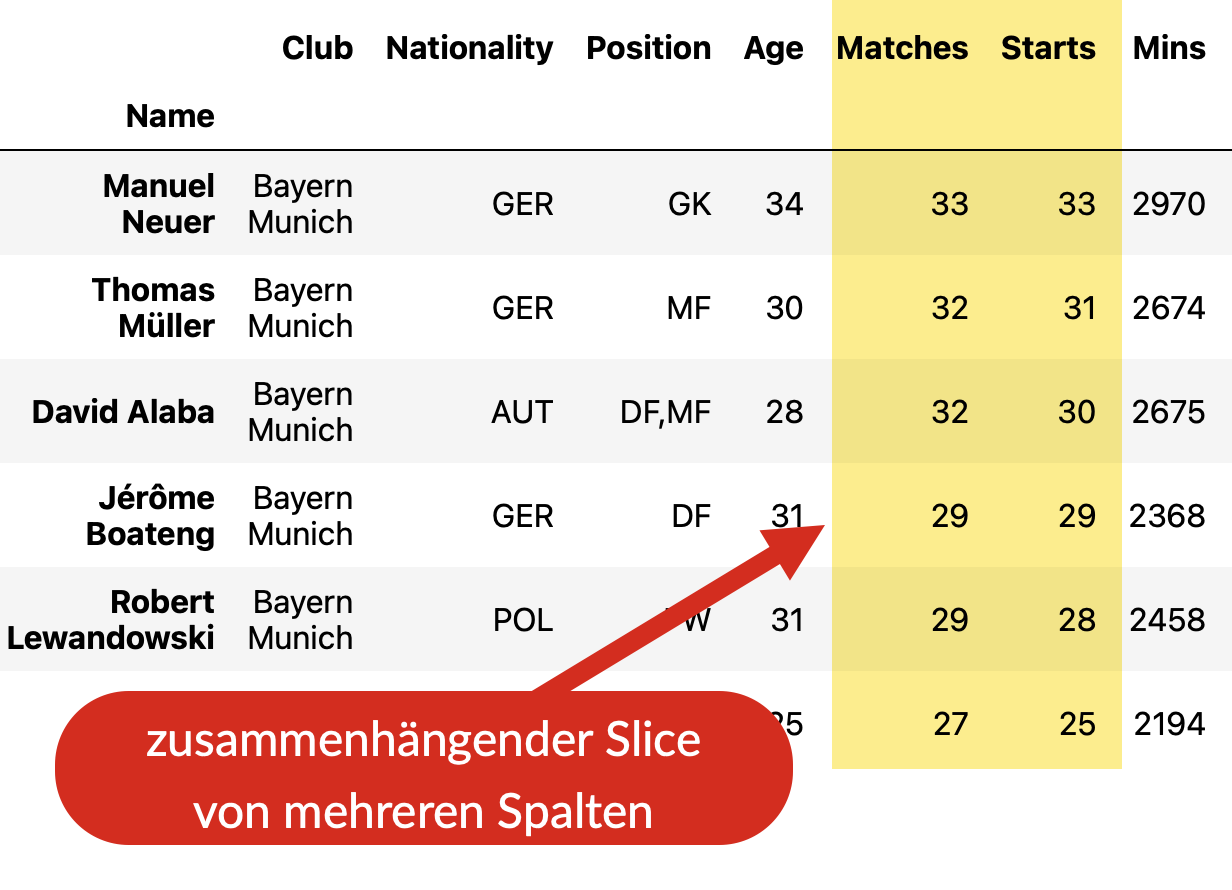
Fig. 14 Auf mehrere zusammenhängende Spalten der Tabelle wird mit .loc[:, start:stopp]
zugegriffen. Das nennt man Slicing.#
Das folgende Beispiel zeigt das Slicing zweier Spalten.
spiele = data.loc[:, 'Matches' : 'Starts']
print(spiele)
Matches Starts
Name
Manuel Neuer 33 33
Thomas Müller 32 31
David Alaba 32 30
Jérôme Boateng 29 29
Robert Lewandowski 29 28
... ... ...
Loris Karius 4 3
Akaki Gogia 7 0
Leon Dajaku 2 0
Tim Maciejewski 1 0
Joshua Mees 1 0
[177 rows x 2 columns]
Zugriff auf Zellen#
Es kann auch vorkommen, dass man gezielt auf eine einzelne Zelle oder einen
Bereich von Zellen zugreifen möchte. Auch dazu benutzen wir das Attribut
.loc[].
Eine Zelle ist ein einzelnes Element der Tabelle, sozusagen der Kreuzungspunkt
zwischen Zeile und Spalte. Die Zelle mit dem Zeilenindex Thomas Müller und dem
Spaltenindex Age enthält das Alter von Thomas Müller.
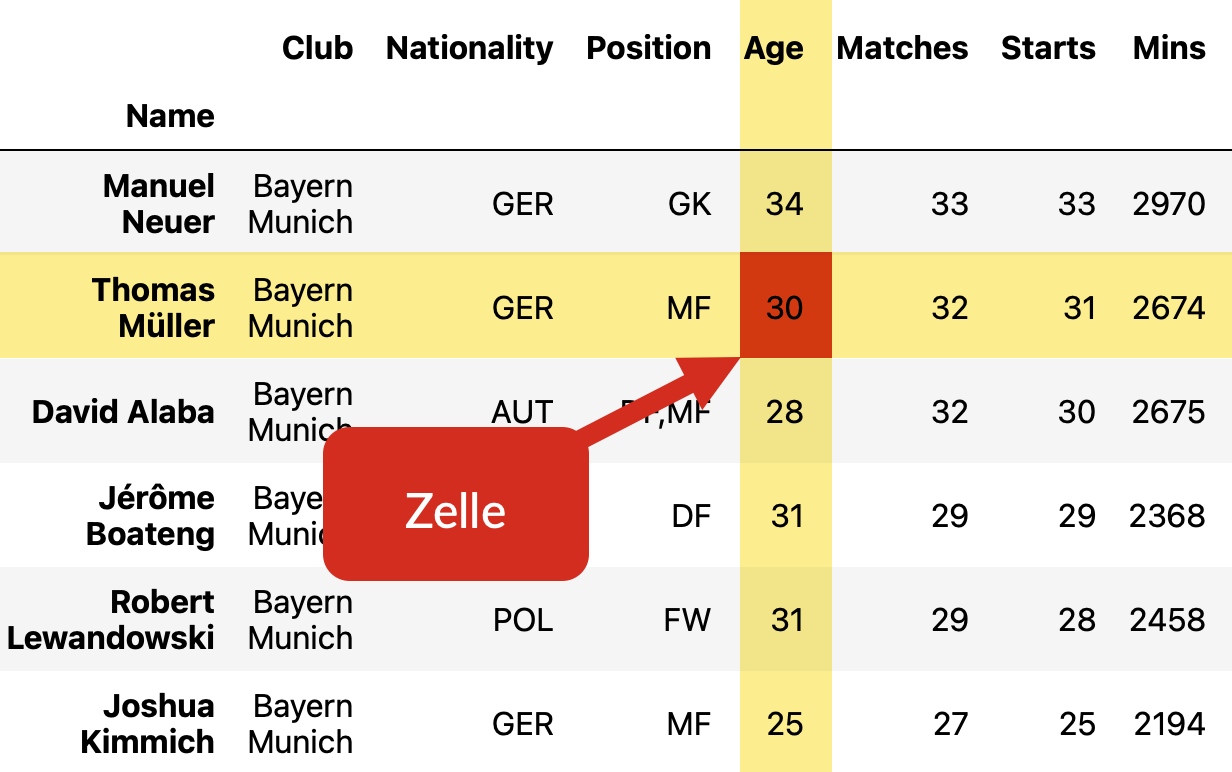
Fig. 15 Auf ein einzelne Zelle der Tabelle wird mit .loc[zeilenindex, spaltenindex] zugegriffen.#
Der Trick ist nun, die drei Möglichkeiten (einzeln, Slice und Selektion per Liste) für die Zeilen mit den gleichen drei Möglichkeiten des Zugriffes für Spalten zu kombinieren.
Wollen wir beispielsweise das Alter von Thomas Müller aus der Tabelle heraussuchen, so gehen wir folgendermaßen vor.
alter_mueller = data.loc['Thomas Müller', 'Age']
print(f'Thomas Müller ist {alter_mueller} Jahre alt.')
Thomas Müller ist 30 Jahre alt.
Wollen wir Beispielsweise das Alter der Fußballprofis von ‘David Alaba’ bis ‘Robert Lewandowski’ wissen, so gehen wir folgendermaßen vor:
alter_slice = data.loc['David Alaba' : 'Robert Lewandowski', 'Age']
print(alter_slice)
Name
David Alaba 28
Jérôme Boateng 31
Robert Lewandowski 31
Name: Age, dtype: int64
Und möchten wir von den Herren Thomas Müller und Joshua Kimmich sowhl die Nationalität als auch das Alter selektieren, so gehen wir wie folgt vor:
spezialauswahl = data.loc[ ['Thomas Müller', 'Joshua Kimmich'], ['Nationality', 'Age'] ]
print(spezialauswahl)
Nationality Age
Name
Thomas Müller GER 30
Joshua Kimmich GER 25
Mini-Übung
Lassen Sie sich das Alter von Robert Lewandowski und Thomas Müller anzeigen.
# Hier Ihr Code
Lösung
alter = data.loc[['Robert Lewandowski', 'Thomas Müller'], 'Age']
print(alter)
Filtern#
Vielleicht haben Sie sich schon gefragt, warum wir nur Bayern-Spieler analysiert
haben. Die Antwort ist simpel, Bayern stand im Datensatz oben in den ersten
Zeilen. Tatsächlich sind aber die Spielerdaten von sieben Vereinen im Datensatz
enthalten. Wir können uns die verschiedenen Werte einer Spalte mit der Methode
.unique() ansehen.
In einem ersten Schritt lesen wir die Spalte mit den Vereinen aus (Spalte
‘Club’). Dann wenden wir auf das Ergnis die Methode .unique() an.
vereine = data.loc[:, 'Club']
vereinsnamen = vereine.unique()
print(vereinsnamen)
['Bayern Munich' 'Borussia Dortmund' 'RB Leipzig' 'Wolfsburg'
'Eintracht Frankfurt' 'Bayer Leverkusen' 'Union Berlin']
Wenn man möchte, kann man auch beide Schritte in einem Schritt ausführen:
vereinsnamen = data.loc[:, 'Club'].unique()
print(vereinsnamen)
['Bayern Munich' 'Borussia Dortmund' 'RB Leipzig' 'Wolfsburg'
'Eintracht Frankfurt' 'Bayer Leverkusen' 'Union Berlin']
Jetzt wo wir wissen, dass auch Eintracht Frankfurt dabei ist, würden wir den Datensatz gerne nach Eintracht Frankfurt filtern. Dazu benutzen wir einen Vergleich und speichern das Ergebnis des Vergleichs in einer Variablen.
filter_eintracht = data.loc[:, 'Club'] == 'Eintracht Frankfurt'
print(filter_eintracht)
Name
Manuel Neuer False
Thomas Müller False
David Alaba False
Jérôme Boateng False
Robert Lewandowski False
...
Loris Karius False
Akaki Gogia False
Leon Dajaku False
Tim Maciejewski False
Joshua Mees False
Name: Club, Length: 177, dtype: bool
Das Ergebnis des Vergleichs, der in der Variablen filter_eintracht gespeichert
ist, ist ein Pandas-Series-Objekt, das für jede Zeile gespeichert hat, ob der
Vergleich wahr (True) oder falsch (False) ist. Ist in einer Zeile der Club
gleich ‘Eintracht Frankfurt’, so ist in dem booleschen Objekt an dieser Stelle
True eingetragen und ansonsten False. Der Datenyp dtype wird mit bool
angegeben.
Wir können nun anstatt einer Liste diesen booleschen Index nutzen, um Zeilen zu
selektieren. Steht in einer Zeile des booleschen Series-Objektes True, so wird
diese Zeile ausgewählt. Ansonsten wird die Zeile übersprungen. Damit erhalten
wir alle Spielerdaten, die zu Eintracht Frankfurt gehören.
eintracht_frankfurt = data.loc[filter_eintracht, :]
print(eintracht_frankfurt)
Club Nationality Position Age Matches \
Name
Kevin Trapp Eintracht Frankfurt GER GK 30 33
André Silva Eintracht Frankfurt POR FW 24 32
Filip Kostić Eintracht Frankfurt SRB DF 27 30
Martin Hinteregger Eintracht Frankfurt AUT DF 27 29
Daichi Kamada Eintracht Frankfurt JPN MF,FW 23 32
Makoto Hasebe Eintracht Frankfurt JPN DF,MF 36 29
Djibril Sow Eintracht Frankfurt SUI MF 23 28
Obite N'Dicka Eintracht Frankfurt FRA DF 20 23
Sebastian Rode Eintracht Frankfurt GER MF 29 27
Erik Durm Eintracht Frankfurt GER DF 28 21
Stefan Ilsanker Eintracht Frankfurt AUT MF,DF 31 27
Tuta Eintracht Frankfurt BRA DF 21 19
Amin Younes Eintracht Frankfurt GER MF,FW 26 26
David Abraham Eintracht Frankfurt ARG DF 34 14
Aymen Barkok Eintracht Frankfurt MAR FW,MF 22 26
Bas Dost Eintracht Frankfurt NED FW 31 12
Luka Jović Eintracht Frankfurt SRB FW,MF 22 18
Almamy Touré Eintracht Frankfurt MLI DF 24 17
Steven Zuber Eintracht Frankfurt SUI DF,MF 28 20
Timothy Chandler Eintracht Frankfurt USA DF 30 15
Dominik Kohr Eintracht Frankfurt GER MF,FW 26 7
Ajdin Hrustic Eintracht Frankfurt AUS MF,FW 24 11
Danny da Costa Eintracht Frankfurt GER DF 27 6
Elias Bördner Eintracht Frankfurt GER GK 18 1
Ragnar Ache Eintracht Frankfurt GER FW,DF 22 7
Starts Mins Goals Assists Penalty_Goals \
Name
Kevin Trapp 33 2970 0 0 0
André Silva 32 2760 28 7 7
Filip Kostić 29 2534 4 14 0
Martin Hinteregger 29 2527 2 1 0
Daichi Kamada 28 2356 5 12 0
Makoto Hasebe 26 2288 0 0 0
Djibril Sow 25 2175 0 2 0
Obite N'Dicka 23 2044 3 1 0
Sebastian Rode 19 1625 1 0 0
Erik Durm 19 1480 1 2 0
Stefan Ilsanker 17 1578 1 0 0
Tuta 16 1459 0 0 0
Amin Younes 16 1391 3 3 0
David Abraham 14 1222 1 0 0
Aymen Barkok 9 977 2 3 0
Bas Dost 9 817 4 2 1
Luka Jović 8 894 4 1 0
Almamy Touré 8 704 1 1 0
Steven Zuber 6 585 0 3 0
Timothy Chandler 3 432 1 0 0
Dominik Kohr 2 260 0 0 0
Ajdin Hrustic 1 272 1 0 0
Danny da Costa 1 110 0 0 0
Elias Bördner 1 90 0 0 0
Ragnar Ache 0 100 1 0 0
Penalty_Attempted xG xA Yellow_Cards Red_Cards
Name
Kevin Trapp 0 0.00 0.00 0 0
André Silva 7 0.79 0.18 1 0
Filip Kostić 0 0.14 0.41 4 0
Martin Hinteregger 0 0.07 0.03 4 0
Daichi Kamada 0 0.21 0.28 3 0
Makoto Hasebe 0 0.01 0.01 5 0
Djibril Sow 0 0.02 0.06 6 0
Obite N'Dicka 0 0.05 0.01 10 0
Sebastian Rode 0 0.01 0.07 10 0
Erik Durm 0 0.10 0.13 1 0
Stefan Ilsanker 0 0.07 0.01 4 0
Tuta 0 0.01 0.02 5 0
Amin Younes 0 0.22 0.11 5 0
David Abraham 0 0.05 0.03 5 1
Aymen Barkok 0 0.15 0.27 5 0
Bas Dost 1 0.47 0.25 3 0
Luka Jović 0 0.28 0.06 2 0
Almamy Touré 0 0.15 0.16 2 0
Steven Zuber 0 0.12 0.29 1 0
Timothy Chandler 0 0.18 0.07 2 0
Dominik Kohr 0 0.19 0.01 1 0
Ajdin Hrustic 0 0.10 0.14 2 0
Danny da Costa 0 0.14 0.00 0 0
Elias Bördner 0 0.00 0.00 0 0
Ragnar Ache 0 0.24 0.00 1 0
Da der print()-Befehl nicht alle Einträge anzeigt, gehen wir jetzt Zeile für
Zeile durch. Den Zeilenindex erhalten wir über das Attribut .index:
for zeilenindex in eintracht_frankfurt.index:
print(zeilenindex)
Kevin Trapp
André Silva
Filip Kostić
Martin Hinteregger
Daichi Kamada
Makoto Hasebe
Djibril Sow
Obite N'Dicka
Sebastian Rode
Erik Durm
Stefan Ilsanker
Tuta
Amin Younes
David Abraham
Aymen Barkok
Bas Dost
Luka Jović
Almamy Touré
Steven Zuber
Timothy Chandler
Dominik Kohr
Ajdin Hrustic
Danny da Costa
Elias Bördner
Ragnar Ache
Zusammenfassung und Ausblick#
In diesem Abschnitt konnten wir nur die Basis-Funktionalitäten streifen. Natürlich ist auch möglich, Bereiche zu sortieren oder gruppieren. Im nächsten Abschnitt erarbeiten wir uns erste statistische Analysen mit Pandas.

