10.3 Ableitung, Integration und Differentialgleichung mit Simulink#
Bei den Modellen treten sehr häufig Differentialgleichungen auf. In diesem Kapitel betrachten wir die Modellierung einer linearen Differentialgleichung 1. Ordnung mit Simulink. Davor sehen wir uns noch zwei Beispiele zur Ableitung und Integration an.
Lernziele#
Lernziele
Sie können eine Funktion in Simulink ableiten.
Sie können eine Funktion in Simulink integrieren.
Sie können eine lineare Differentialgleichung 1. Ordnung mit Simulink-Blöcken modellieren.
Ableitung am Beispiel der Sinusfunktion#
In dem folgenden Simulink-Modell modellieren wir die 1. Ableitung der
Sinus-Funktion. Dazu wählen wir einen Sine-Block als Eingangssignal,
verarbeiten diesen durch den Derivative-Block (Derivative ist das englische
Wort für Ableitung) und geben anschließend das Ergebnis über den Scope-Block
aus. In Simulink sieht das Modell dann folgendermaßen aus:
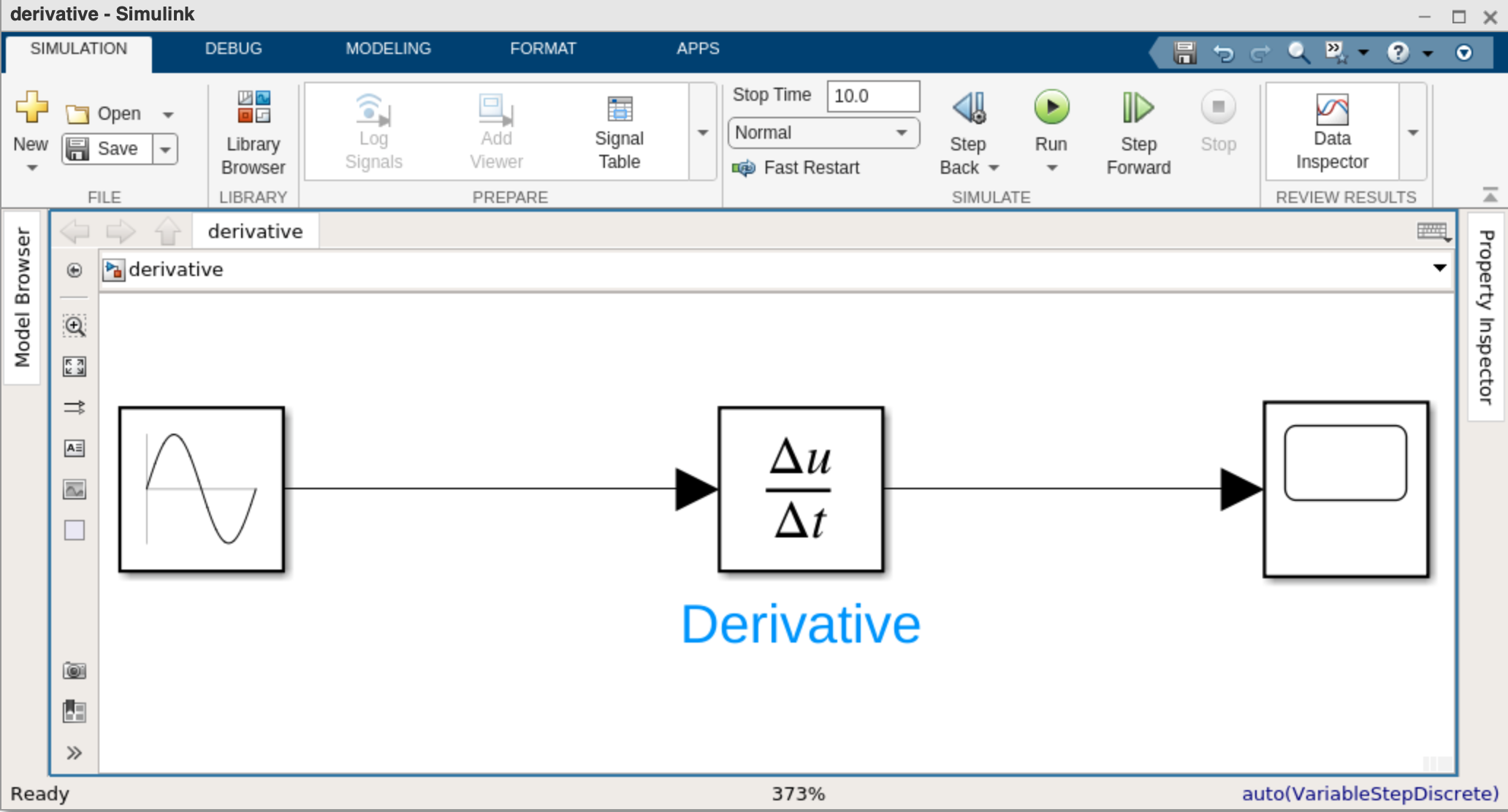
Wenn Sie sich nun das Ergebnis der Ableitung durch Doppelklick auf den Scope-Block ansehen, haben Sie folgende Ansicht:
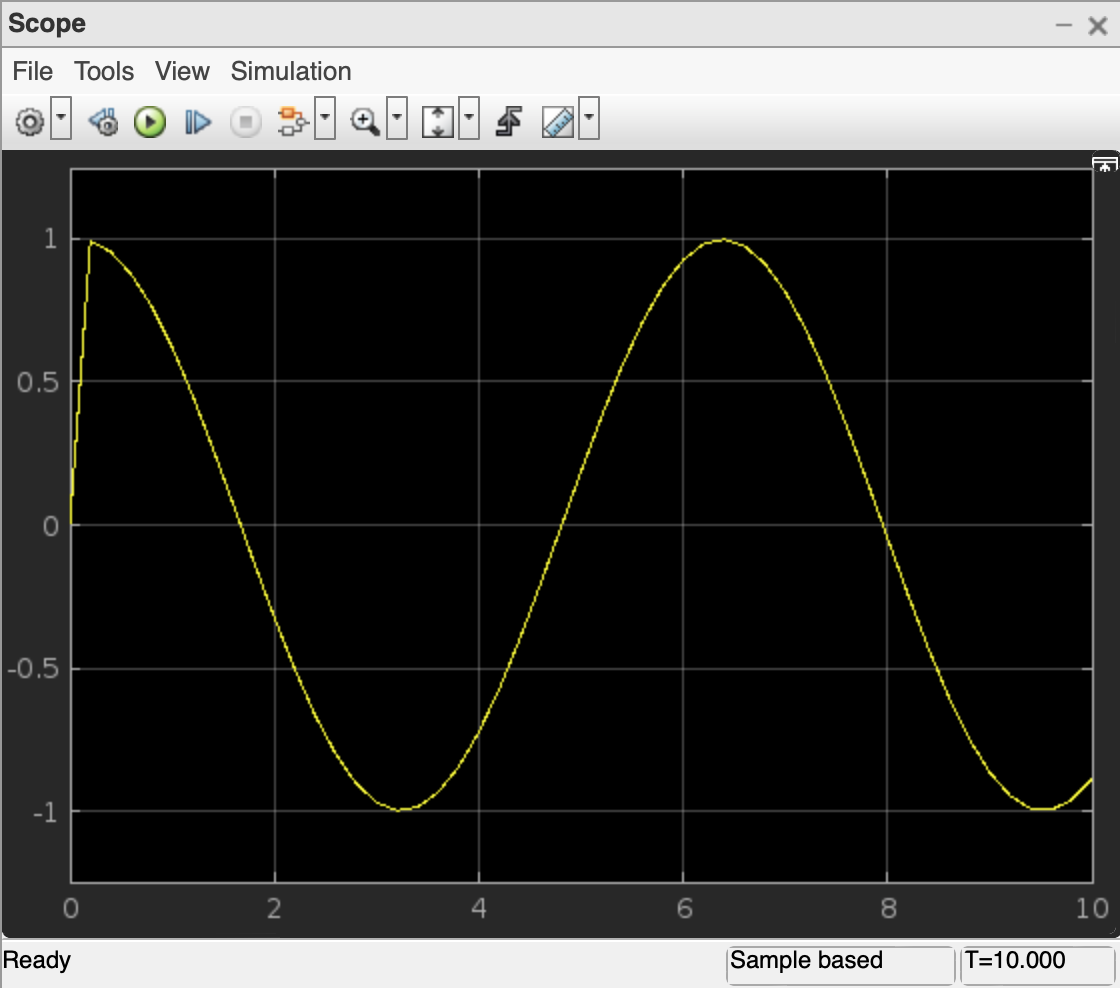
Auf der einen Seite zeigt das Liniendiagramm die Kosinus-Funktion wie erwartet. Auf der anderen Seite scheint es gerade am Anfang bei \(t=0\) eine Unstimmigkeit zu geben. Woher kommt das?
MATLAB und Simulink sind numerische Softwaretools. Im Gegensatz zu Computer-Algebra-Systemen wie WolframAlpha oder GeoGebra können sie nicht die Lösung einer Gleichung oder eine Ableitung symbolisch berechnen. Stattdessen ermitteln sie Lösung der mathematischen Probleme numerisch. Computer-Algebra-Systeme gehen wie Menschen cor. Das Symbol “hoch 2” wird manipuliert “hoch 1” (Regel: beim Ableiten einer Potenz wird es eins weniger) und als Vorfaktor davor geschrieben. Weil Symbole manipuliert werden, heißt diese Lösungsmethode symbolisch. Stattdessen erstellt MATLAB eine Wertetabelle der Funktion, die abgeleitet werden soll. Danach geht MATLAB diese Tabelle Stück für Stück durch und bildet zwischen dem ersten und dem zweiten Punkt das Steigungsdreieck, dann zwischen dem zweiten und dem dritten Punkt und immer so weiter. Danach zeichnet MATLAB bzw. Simulink die Liste der Steigungen der Steigungsdreiecke und hat damit eine Näherung der 1. Ableitung gefunden.
Integration am Beispiel der Wurzelfunktion#
Als nächstes Beispiel wollen wir die Funktion
integrieren. Das Ergebnis ist eigentlich \(U(t) = \frac{2}{3} t^{3/2} + C\), aber standardmäßig wird die Integrationskonstante auf Null gesetzt, also \(C = 0\).
Um das Eingangssignal \(t\) zu erzeugen, verwenden wir wiederum den Ramp-Block.
Danach stecken wir \(t\) in die Wurzelfunktion. Die Wurzelfunktion gehört zu den
Math Operations, der entsprechende Block heißt sqrt-Block. Verbinden wir
beide Blöcke, so erzeugen wir insgesamt \(\sqrt{t}\).
Nun integrieren wir das Eingangssignal mit dem Integrator-Block, der sich in
der Bibliothek Continuos befindet. Das Ergebnis visualisieren wir mit einem
Scope-Block.
Das fertige Blockdiagramm zeigt der folgende Screenshot.
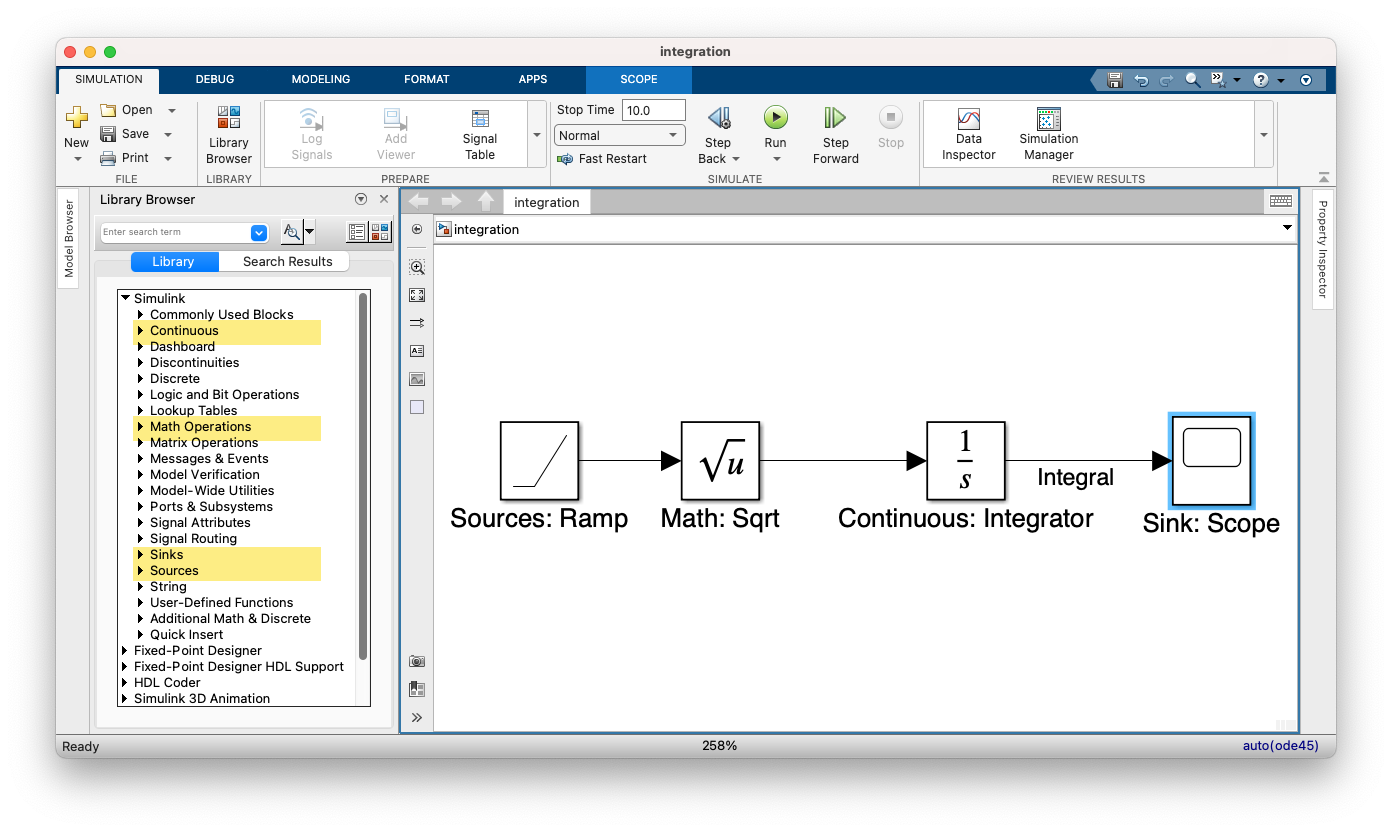
Lineare Differentialgleichungen 1. Ordnung#
Nun schauen wir uns noch am Beispiel der folgenden linearen Differentialgleichung 1. Ordnung
an, wie in Simulink die numerische Lösung der Differentialgleichung konstruiert wird.
Dazu werden nacheinander die Blöcke
Sources \(\rightarrow\) Constant
Math Operations \(\rightarrow\) Add
Continuous \(\rightarrow\) Integrator
Commonly Used Blocks \(\rightarrow\) Gain
Sinks \(\rightarrow\) Scope
in den Arbeitsbereich gezogen und wie in den folgenden Screenshots rot markiert verbunden. Zuletzt ermöglicht der Start der Simulation eine Visualisierung der numerischen Lösung über die Scope-Ausgabe.
Die folgende Sequenz an Screenshots zeigt nacheinander die notwendigen Schritte, um die Differentialgleichung
zu modellieren.
Zusammenfassung#
Dieser kurze Einstieg in Simulink kann nur der Anfang sein. Wenn Sie Simulink vertiefen wollen, bietet Mathworks zahlreiche (englischsprachige) Tutorials an.

