Übungen

Übung 9.1

Laden Sie die Datei 20220801_Marktwert_Bundesliga.csv herunter. Die ersten 5 Zeilen sind Kommentare, die beim Einlesen übersprungen werden sollten.

1. Verschaffen Sie sich erst einen Überblick über die Daten.

2. Filtern Sie dann die Daten nach der Ligazugehörigkeit (‘Bundesliga’, ‘2. Bundesliga’ und ‘3. Liga’).

3. Lassen Sie dann für jede der drei Ligen den Wert der Vereine visualisieren.

Lösung

import matplotlib.pyplot as plt
import pandas as pd

# Import der Tabelle
data = pd.read_csv('20220801_Marktwert_Bundesliga.csv', skiprows=5, index_col=0)

# Überblick
print(data.info())
print(data.describe())

# Filtern nach den drei Ligen
erste_bundesliga = data[ data.loc[:, 'Ligazugehörigkeit'] == 'Bundesliga' ]
zweite_bundesliga = data[ data.loc[:, 'Ligazugehörigkeit'] == '2. Bundesliga' ]
dritte_bundesliga = data[ data.loc[:, 'Ligazugehörigkeit'] == '3. Liga' ]

# 1. Bundesliga
x = erste_bundesliga.index
y = erste_bundesliga.loc[:, 'Wert']

plt.figure()
plt.bar(x,y)
plt.xticks(rotation=45, ha='right')
plt.xlabel('Verein')
plt.ylabel('Wert')
plt.title('Erste Bundesliga');

# 2. Bundesliga
x = zweite_bundesliga.index
y = zweite_bundesliga.loc[:, 'Wert']

plt.figure()
plt.bar(x,y)
plt.xticks(rotation=45, ha='right')
plt.xlabel('Verein')
plt.ylabel('Wert')
plt.title('Zweite Bundesliga');

# 3. Bundesliga
x = dritte_bundesliga.index
y = dritte_bundesliga.loc[:, 'Wert']

plt.figure()
plt.bar(x,y)
plt.xticks(rotation=45, ha='right')
plt.xlabel('Verein')
plt.ylabel('Wert')
plt.title('Dritte Bundesliga');

Übung 9.2

Verwenden Sie nun die Daten aus der vorherigen Übung, um die Kadergröße der Vereine zu visualisieren. Lassen Sie für jede Liga ein eigenes Diagramm generieren, das die Kadergröße für jeden Verein zeigt. Zudem soll jeweils der Mittelwert als rote horizontale Linie und die Standardabweichung als Fehlerbalken dargestellt werden.

Lösung

import matplotlib.pyplot as plt
import pandas as pd

# Import der Tabelle
data = pd.read_csv('20220801_Marktwert_Bundesliga.csv', skiprows=5, index_col=0)

# Filtern nach den drei Ligen
erste_bundesliga = data[ data.loc[:, 'Ligazugehörigkeit'] == 'Bundesliga' ]
zweite_bundesliga = data[ data.loc[:, 'Ligazugehörigkeit'] == '2. Bundesliga' ]
dritte_bundesliga = data[ data.loc[:, 'Ligazugehörigkeit'] == '3. Liga' ]

# Visualisierung 1. Bundesliga
x = erste_bundesliga.index
y = erste_bundesliga.loc[:, 'Kadergröße']
mittelwert = y.mean()
standardabweichung = y.std()

plt.figure()
plt.errorbar(x,y, yerr=standardabweichung, fmt='o')
plt.axhline(mittelwert, color='red')
plt.xticks(rotation=45, ha='right')
plt.xlabel('Verein')
plt.ylabel('Kadergröße')
plt.title('Erste Bundesliga');

# Visualisierung 2. Bundesliga
x = zweite_bundesliga.index
y = zweite_bundesliga.loc[:, 'Kadergröße']
mittelwert = y.mean()
standardabweichung = y.std()

plt.figure()
plt.errorbar(x,y, yerr=standardabweichung, fmt='o')
plt.axhline(mittelwert, color='red')
plt.xticks(rotation=45, ha='right')
plt.xlabel('Verein')
plt.ylabel('Kadergröße')
plt.title('Zweite Bundesliga');

# Visualisierung 3. Liga
x = dritte_bundesliga.index
y = dritte_bundesliga.loc[:, 'Kadergröße']
mittelwert = y.mean()
standardabweichung = y.std()

plt.figure()
plt.errorbar(x,y, yerr=standardabweichung, fmt='o')
plt.axhline(mittelwert, color='red')
plt.xticks(rotation=45, ha='right')
plt.xlabel('Verein')
plt.ylabel('Kadergröße')
plt.title('Dritte Bundesliga');

Übung 9.3

Teilaufgabe 1:

Programmieren Sie eine Funktion, die einen Random Walk mit dem Turtle-Modul implementiert (siehe Übung 7.4). Der Roboter soll 100x zufällig eine Richtung Osten, Süden, Westen oder Norden wählen und dann 10 Schritte laufen. Lassen Sie dann den Abstand zum Ursprung berechnen und von der Funktion zurückgeben.

Tipp: Die aktuelle Position des Roboters kann mit der Methode .position() bestimmt werden. Die Anweisung x,y = robo.position() speichert die x-Position in x und entsprechend die y-Position in y, wenn Ihr Roboter robo heißt.

Teilaufgabe 2:

Lassen Sie nun den Roboter 10 x seinen Random Walk ausführen und jeweils die Entfernung zum Ursprung zurückgeben. Sammeln Sie die Entfernungen in einer Liste. Untersuchen Sie mit einem Histogramm, wie die Entfernungen verteilt sind. Wenn die Rechenzeiten auf Ihrer Hardware annehmbar sind, erhöhen Sie bitte die Anzahl der Random Walks (vorsichtig!).

Tipp: Setzen Sie innerhalb der Random-Walk-Funktion die Geschwindigkeit des Roboters auf 0, also robo.speed(0), falls Ihr Roboter robo heißt. Fügen Sie außerdem nach der letzten Bewegung den Befehl robo.done()ein. Dann wird die Bewegung nicht mehr animiert und nur der Laufweg angezeigt.

Lösung

Teilaufgabe 1: Implementierung eines Random Walks als Funktion

import ColabTurtlePlus.Turtle as turtle
import numpy as np

def random_walk():
    robo = turtle.Turtle()
    robo.speed(0)
    for i in range(100):
        zufallswinkel = np.random.randint(3) * 90
        robo.left(zufallswinkel)
        robo.forward(10)

    x,y = robo.position()
    robo.done()
    
    entfernung = np.sqrt(x**2 + y**2)
    return entfernung

Teilaufgabe 2: Durchführung von vielen Random Walks und Sammeln der Entfernungen in einer Liste (hier 500 Randon Walks):

turtle.clearscreen()
    
liste_entfernungen = []
for i in range(500):
    d = random_walk()
    liste_entfernungen.append(d)

Das Ergebnis könnte beispielhaft so aussehen:

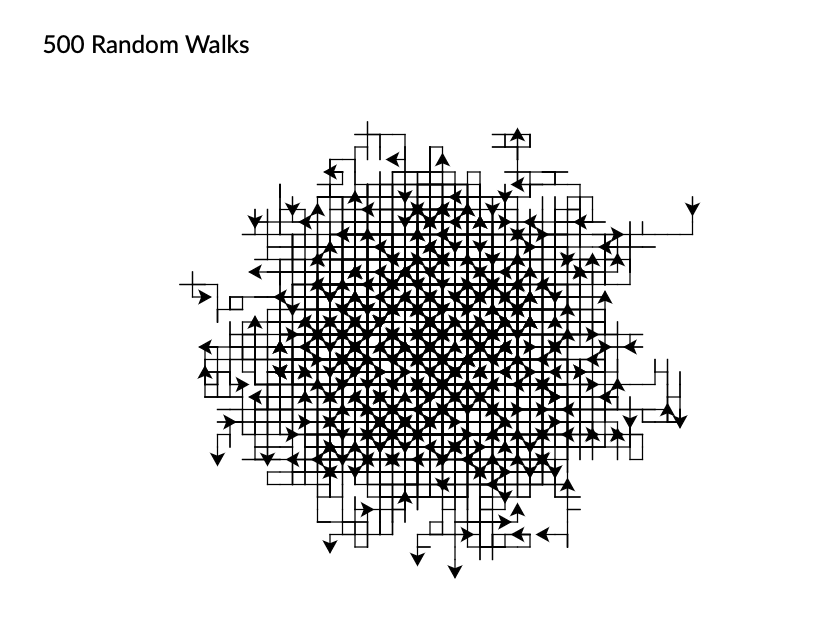
Fig. 12 Endergebnis von 500 Random Walks

Der Code zur Erzeugung des Histogramms ist:

import matplotlib.pyplot as plt

plt.figure()
plt.hist(liste_entfernungen, bins=25)
plt.xlabel('Entfernung zum Ursprung in px')
plt.ylabel('Häufigkeit')
plt.title('Analyse der Random Walks');

Das Histogramm könnte beispielhaft so aussehen:

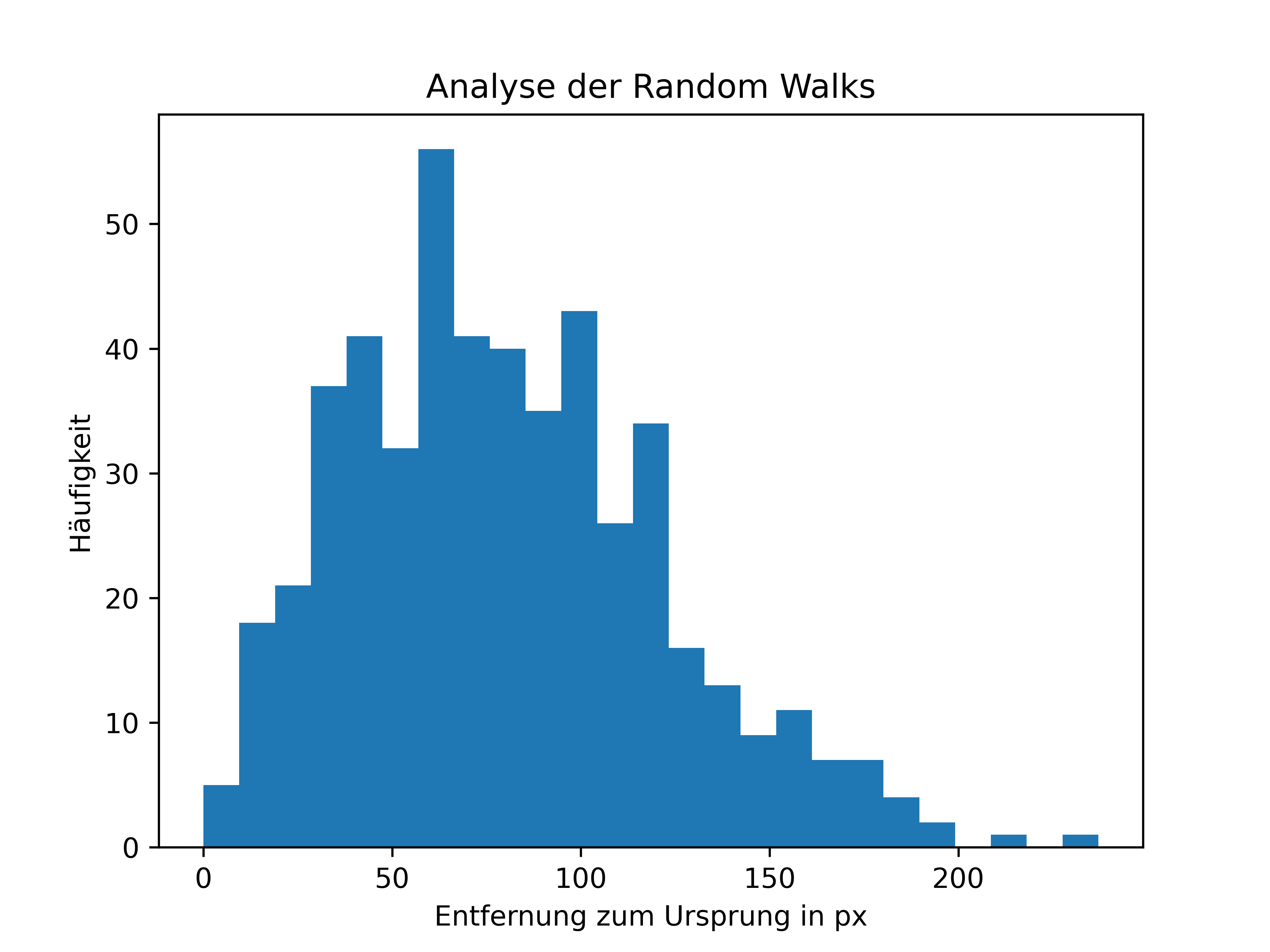
Fig. 13 Histogramm der 500 Random Walks

Die Entfernungen sind nicht gleichverteilt und auch nicht normalverteilt.