3.1 Koordinaten und Koordinatensysteme#
In den Ingenieurwissenschaften ist es essentiell, die Position von Objekten und die auf sie wirkenden Kräfte präzise zu beschreiben. Dieses Kapitel widmet sich dem mathematischen Konzept, Positionen im Raum zu definieren. Dazu wird zuerst der Fachbegriff Tupel eingeführt. Tupel, die auf ein Koordinatensystem bezogen werden, heißen Koordinaten. Sie ermöglichen es uns, Positionen genau festzulegen.
Lernziele#
Lernziele
Sie können mit eigenen Worten erklären, was ein n-Tupel ist.
Sie wissen, was Koordinaten sind.
Sie können erklären, was ein Koordinatensystem ist.
Sie kennen das zweidimensionale und dreidimensionale kartesische Koordinatensystem.
Sie können bei dreidimensionalen kartesischen Koordinatensystemen ein Rechtssystem von einem Linkssystem unterscheiden.
Sie können Punkte in ein Polarkoordinatensystem einzeichnen und daraus ablesen.
Tupel und Koordinaten#
Um eine Position anzugeben, verwenden wir Koordinaten in einem Bezugssystem. Ein einfaches Beispiel hierfür ist ein Schachbrett, auf dem die Position der Felder durch Buchstaben (A bis H) und Zahlen (1 bis 8) gekennzeichnet wird. Die Angabe „Turm auf D3“ beschreibt die genaue Position der Schachfigur.
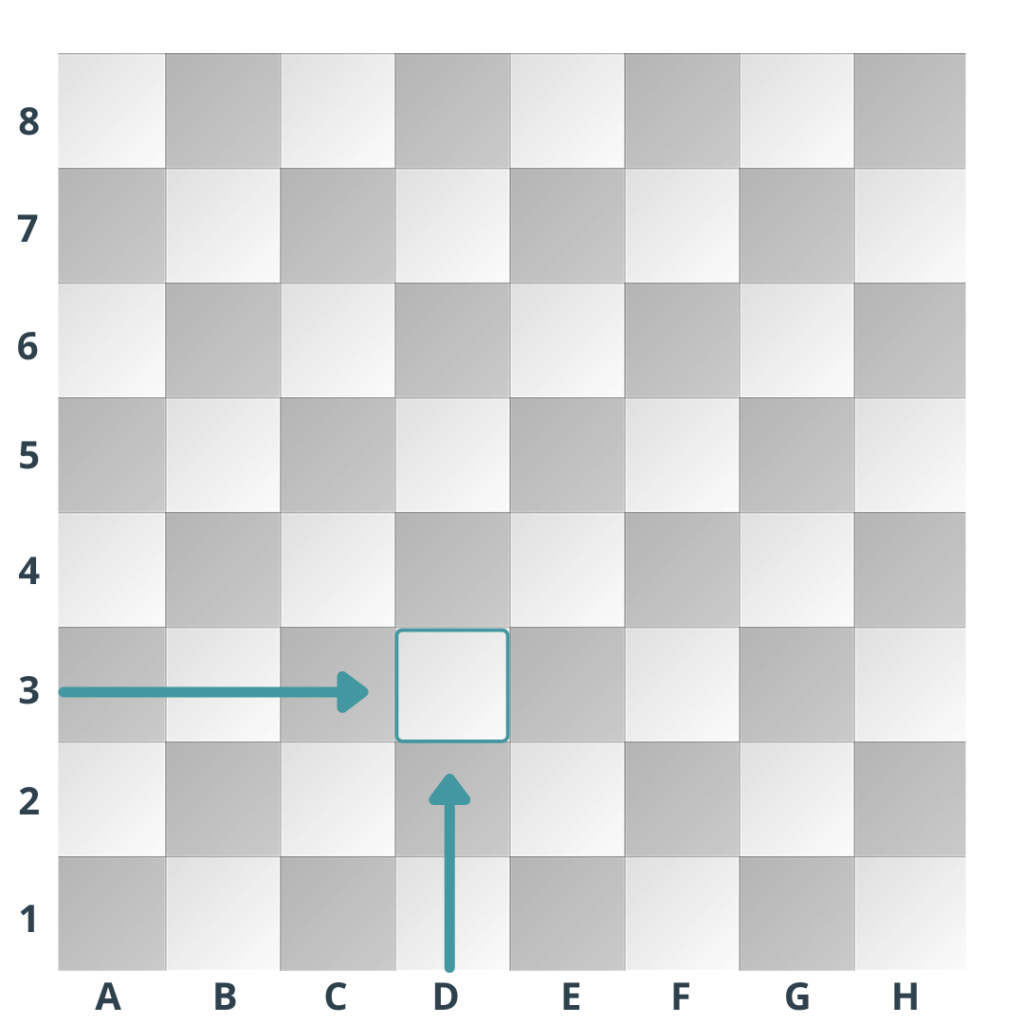
Fig. 1 Quelle: https://schachliebe.de/schach-aufstellung/#
Um die Schachfigur korrekt zu platzieren, benötigen wir zwei Angaben: „D“ steht für die vierte Linie von links und „3“ für die dritte Reihe von unten. Diese beiden Angaben nennt man Koordinaten.
Für die Angabe der Position eines Gebäudes, beispielsweise des Hörsaals 8/209, benötigen wir drei Koordinaten.
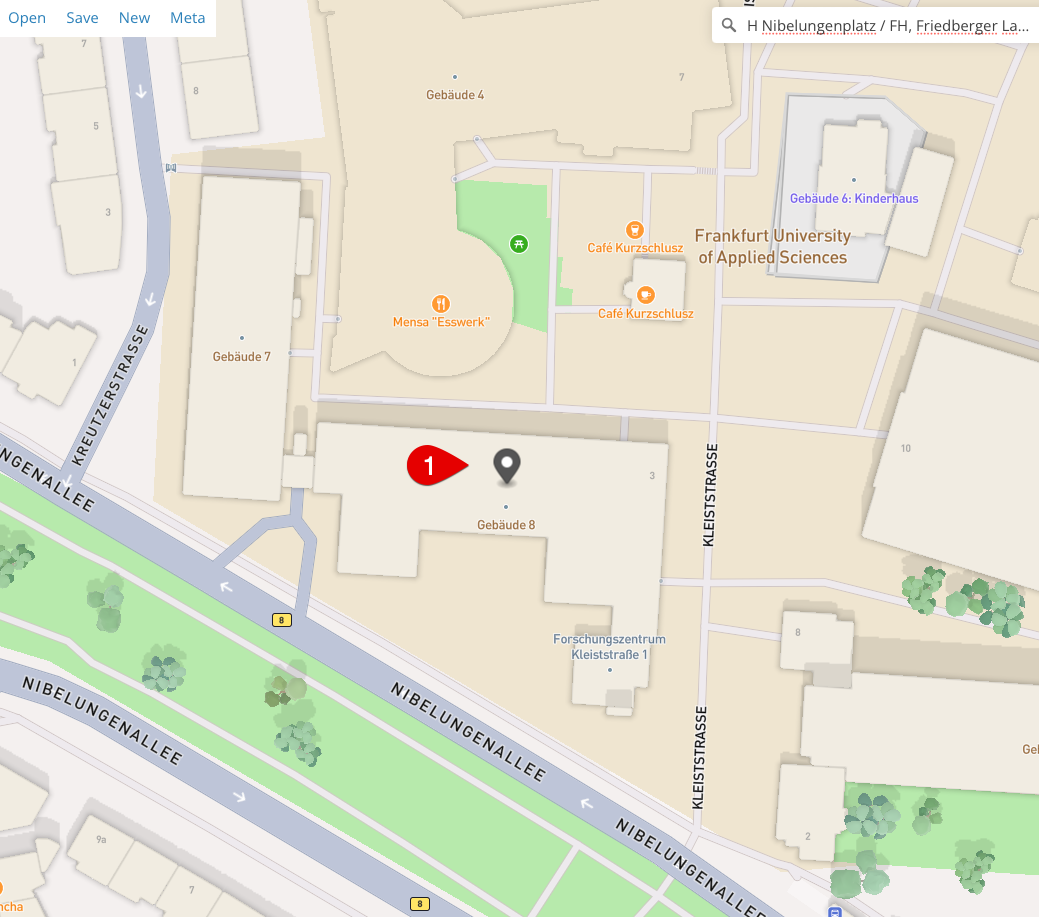
Fig. 2 Gebäude 8 der Frankfurt UAS#
Das Gebäude 8 der Frankfurt UAS befindet sich auf dem Längengrad 8.691847, dem Breitengrad 50.130161 (beides in Dezimalgrad angegeben) und bei ca. 112 m über Normalhöhennull. Wenn wir die Reihenfolge Längengrad, Breitengrad und Höhe vereinbaren, können wir die Position als Tripel notieren:
Der Begriff Tripel zeigt, dass die Reihenfolge der Zahlen festgelegt und nicht austauschbar ist. Allgemein bezeichnet man eine geordnete Liste von Zahlen (oder anderen mathematischen Objekten) als Tupel. Ein Tupel kann beliebig viele Elemente enthalten, wobei die Anzahl der Elemente dem Begriff vorangestellt wird: Ein Paar \((2 | -3)\) ist ein 2-Tupel, ein Tripel \((8.6, 50.1, 112)\) ist ein 3-Tupel, und ein Quadrupel \((-0.1\,|\,\pi\,|\,3\,| -8)\) ist ein Beispiel für ein 4-Tupel.
Was ist … ein n-Tupel?
Ein n-Tupel ist eine Liste von \(n\) mathematischen Objekten (meistens Zahlen), bei der die Reihenfolge festgelegt ist. Sie werden mit runden Klammern notiert und durch senkrechte Striche oder Kommas getrennt. Ein 2-Tupel wird Paar genannt, ein 3-Tupel Tripel.
n-Tupel haben vielfältige Anwendungen. Beispielsweise könnte eine Firma ein Zeiterfassungssystem einführen, bei dem jede Woche die Anzahl der Arbeitsstunden notiert wird. Ein 7-Tupel \((8, 8, 6, 0, 10, 8, 0)\) könnte bedeuten, dass eine Person am Montag, Dienstag und Samstag jeweils 8 Stunden gearbeitet hat, am Mittwoch 6 Stunden, am Freitag 10 Stunden, und am Donnerstag sowie Sonntag arbeitsfrei hatte.
Wird ein Tupel zur Beschreibung der Position eines Objektes verwendet, nennt man die Elemente des Tupels Koordinaten. In diesem Kontext ist es wichtig, genau zu wissen, auf welches Element sich jede Zahl bezieht. Dies führt uns zum Begriff des Koordinatensystems, der im folgenden Abschnitt näher erläutert wird. Zuerst halten wir jedoch noch die Definition von Koordinaten fest.
Was sind … Koordinaten?
Zur Beschreibung der Position eines Objektes werden Tupel verwendet. Die Elemente eines solchen Tupels werden Koordinaten genannt.
Den Begriff Koordinatensystem haben wir intuitiv verwendet. Was genau ein Koordinatensystem ist, wird im folgenden Abschnitt näher erläutert.
Kartesische Koordinatensysteme#
Ein Koordinatensystem ist ein mathematisches Konzept, das verwendet wird, um die Position von Objekten im Raum eindeutig zu bestimmen. Zur Festlegung eines Koordinatensystems benötigen wir einen festen Bezugspunkt, den sogenannten Ursprung. Der Ursprung wird häufig mit dem Symbol \(O\) (für englisch »Origin«) abgekürzt.
Durch den Ursprung verlaufen die Koordinatenachsen, spezielle Geraden, die die Richtungen im Raum definieren. Wenn zwei Koordinatenachsen senkrecht zueinander stehen, spricht man von einem kartesischen Koordinatensystem.
Das einfachste kartesische Koordinatensystem ist die Zahlengerade im eindimensionalen Raum. In der zweidimensionalen Ebene werden die Achsen üblicherweise mit \(x\) und \(y\) bezeichnet. Alternativ können sie auch als \(x_1\)-Achse und \(x_2\)-Achse benannt werden.
Fig. 3 Eindimensionales kartesisches Koordinantensystem (oben) und zweidimensionales Koordinatensystem (unten), Quelle: Wikimedia Commons von Ag2gaeh, Lizenz: CC BY-SA 4.0#
Zur Beschreibung von Positionen im dreidimensionalen Raum benötigen wir ein 3-Tupel und ein Koordinatensystem mit drei Koordinatenachsen, oft bezeichnet als \(x\)-Achse, \(y\)-Achse und \(z\)-Achse. Alternativ können sie auch als \(x_1\)–Achse, \(x_2\)-Achse und \(x_3\)-Achse bezeichnet werden.
Fig. 4 Dreidimensionales kartesisches Koordinatensystem, Quelle: Wikimedia Commons von Cronholm144, Lizenz: gemeinfrei#
Es gibt zwei Möglichkeiten, die Orientierung der Koordinatenachsen in einem dreidimensionalen kartesischen Koordinatensystem zu wählen:
Rechtssystem
Linkssystem
Im Rechtssystem wird die Orientierung der Achsen durch die rechte Hand definiert: Der Daumen zeigt entlang der ersten Achse, der Zeigefinger entlang der zweiten Achse und der Mittelfinger entlang der dritten Achse. Durch das Abspreizen dieser drei Finger lässt sich ein rechtshändiges Koordinatensystem nachbilden.
Im Linkssystem wird die Orientierung der Achsen durch die linke Hand definiert: Der Daumen zeigt entlang der ersten Achse, der Zeigefinger entlang der zweiten Achse und der Mittelfinger entlang der dritten Achse. Diese Methode erzeugt ein linkshändiges Koordinatensystem.
Was ist … ein kartesisches Koordinatensystem?
Bei einem kartesischen Koordinatensystem stehen jeweils zwei Koordinatenachsen zueinander senkrecht und schneiden sich im Ursprung \(O\).
Das kartesische Koordinatensystem ist eines der grundlegendsten und am häufigsten verwendeten Werkzeuge in der Mathematik und den Ingenieurwissenschaften. Es ermöglicht eine präzise und einfache Darstellung von Punkten und Bewegungen im Raum.
Polarkoordinatensystem#
In den Ingenieurwissenschaften und der Physik wird häufig das Polarkoordinatensystem verwendet, insbesondere wenn es um kreisförmige Phänomene geht. Dieses Koordinatensystem ist besonders nützlich, wenn die Position eines Punktes durch einen Abstand und einen Winkel relativ zu einem festen Punkt beschrieben werden kann.
Zunächst wird ein Ursprung festgelegt, der üblicherweise als Pol bezeichnet wird. Vom Pol ausgehend wird ein Strahl in eine Richtung fesgelegt, die dann als Polarachse bezeichnet wird. Die Position eines Punktes wird in Polarkoordinaten dann durch ein Paar \((r, \varphi)\) beschrieben, wobei
\(r\) der Abstand des Punktes zum Pol/Ursprung und
\(\varphi\) der Winkel relativ zur Polarachse ist.
Fig. 5 Polarkoordinatensystem, Quelle: eigene Darstellung, Lizenz: CC BY-SA 4.0#
Alternativ kann der Winkel relativ zur Polarachse auch im Bogenmaß angegeben werden.
Zusammenfassung und Ausblick#
In diesem Kapitel haben wir die Grundlagen von Koordinatensystemen behandelt. Wir haben den Begriff des Tupels eingeführt und gezeigt, wie Koordinaten und Koordinatensysteme verwendet werden, um Positionen zu beschreiben. Dabei haben wir uns insbesondere das kartesische und das Polarkoordinatensystem angesehen.
Im nächsten Kapitel erweitern wir das Thema, indem wir lernen, wie Tupel durch Rechenoperationen zu Vektoren werden. Der Vektorbegriff ist zentral für die Beschreibung von Kräften und Bewegungen im Raum und bildet die Grundlage für das Verständnis von Vektorräumen.
