6.6 Transponierte und symmetrische Matrizen#
Die Nullmatrix, Diagonalmatrix und die Einheitsmatrix haben wir bereits kennengelernt. Nun lernen wir weitere besondere Matrizen kennen, die transponierte Matrix und die symmetrische Matrix.
Lernziele#
Lernziele
Sie wissen, was eine transponierte Matrix ist und können zu einer gegebenen Matrix die transponierte Matrix berechnen.
Sie kennen die Rechenregeln für transponierte Matrizen.
Sie können überprüfen, ob eine Matrix symmetrisch oder antisymmetrisch/schiefsymmetrisch oder nichts davon ist.
Sie können eine Matrix in einen symmetrischen und antisymmetrischen Teil zerlegen.
Transponierte Matrix#
Eine transponierte Matrix entsteht, indem man die Zeilen und die Spalten einer Matrix vertauscht. Gegeben sei beispielsweise die Matrix
Diese Matrix hat die Dimension \(3\times 2\), also drei Zeilen und zwei Spalten. Die ttansponierte Matrix hat dann zwei Zeilen und drei Spalten. Die erste Zeile wird zur ersten Spalte, die zweite Zeile zur zweiten Spalte und die dritte Zeile zur dritten Spalte. Insgesamt erhalten wir fúr die transponierte Matrix den Ausdruck
Die transponierte Matrix von \(\mathbf{A}\) wird mit einem großen “T” bezeichnet, also als \(\mathbf{A}^{T}\). Manchmal wird auch ein kleines “t” verwendet, also \(\mathbf{A}^{t}\). Der Vorgang des Zeilen-Spalten-Tauschens wird Transponieren genannt.
Transponieren wir \(\mathbf{A}^{T}\) erneut, erhalten wir die ursprüngliche Matrix \(\mathbf{A}\), wie die folgende Animation zeigt.
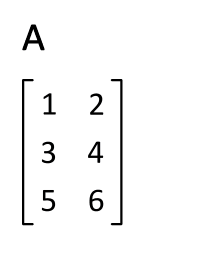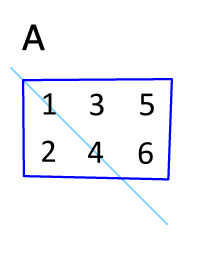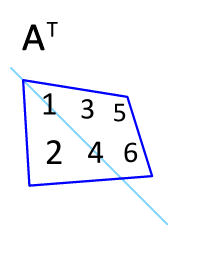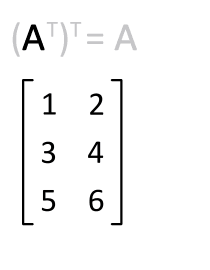
Fig. 18 Transponieren einer Matrix, Quelle: Von Lucas Vieira, Wikimedia Commons, Lizenz: gemeinfrei#
Video “Transponierte Matrizen” von Mathematische Methoden
Rechenregeln für transponierte Matrizen#
Eine Rechenregel für das zweifache Transponieren einer Matrix haben wir oben schon als Animation gesehen. Wir halten fest: wird eine Matrix zweimal transponiert, so ist das Ergebnis die ursprüngliche Matrix, also
Als nächstes betrachten wir die Matrizenaddition und die Skalarmultiplikation in Verbindung mit dem Transponieren. Transponieren wir eine Summe von Matrizen, können wir auch erst die Matrizen einzeln transponieren und dann die Summe berechnen. In Formelschreibweise gilt also
Auch bei der Skalarmultiplikation ist es irrelevant, ob von dem Ergebnis nach der Skalarmultiplikation die transponierte Matrix berechnet wird oder vor der Skalarmultiplikation:
Wiederum ist es die Matrizenmultiplikation, die sich besonders verhält. Bei der Matrizenmultiplikation ändert sich die Reihenfolge beim Multiplizieren:
Symmetrische und antisymmetrische Matrizen#
Eine weitere besondere Matrix ist die symmetrische Matrix. Man nennt eine quadratische Matrix \(\mathbf{A}\) symmetrisch, wenn das Element \(a_{ij}\) der i-ten Zeile und der j-ten Spalte mit dem Element \(a_{ji}\) der j-ten Zeile und der i-ten Spalte übereinstimmt. Eine symmetrische Matrix ist also spiegelsymmetrisch bezüglich der Hauptdiagonalen. Beispielsweise ist die folgende Matrix symmetrisch:
Mit Hilfe der Definition der transponierten Matrix können wir eine symmetrische Matrix auch folgendermaßen spezifizieren.
Was ist … eine symmetrische Matrix?
Eine quadratische Matrix \(\mathbf{A}\) ist symmetrisch, wenn
gilt, wobei \(\mathbf{A}^{T}\) die transponierte Matrix von \(\mathbf{A}\) bezeichnet.
Oder anders ausgedrückt: der Prozess des Transponieren ändert die Matrix nicht.
Sind zwei Matrizen symmetrisch, dann ist auch ihre Summe wieder symmetrisch, denn es gilt
Das gilt auch für eine Matrix, die mit einem Skalar multipliziert wird. Bei der Skalarmultiplikation bleibt die Symmetrie erhalten. Anders sieht es wieder einmal aus, wenn wir die Matrizenmultiplikation betrachten.
Im Allgemeinen gilt für symmetrische Matrizen
Nur wenn für die beiden Matrizen \(\mathbf{A}\) und \(\mathbf{B}\) zufälligerweise \(\mathbf{A}\cdot\mathbf{B} = \mathbf{B}\cdot\mathbf{A}\) gilt, ist auch die Produktmatrix symmetrisch.
Video “Symmetrische Matrizen” von Mathematische Methoden
Der Gegenpart zu einer symmetrischen Matrix ist die antisymmetrische Matrix. Eine Matrix wird antisymmetrisch genannt, wenn die Eigenschaft
erfüllt ist. Für alle Elemente der Matrix gilt also \(a_{ij} = - a_{ji}\). Manchmal wird eine solche Matrix auch schiefsymmetrische Matrix genannt.
Ein Beispiel für eine schiefsymmetrische Matrix ist die Matrix
Zerlegung in symmetrische und antisymmetrische Matrix#
Für quadratische Matrizen können wir eine Zerlegung der Matrix in ihren symmetrischen Anteil und ihren antisymmetrischen Anteil vornehmen. Zunächst aber halten wir fest: wird eine quadratische Matrix \(\mathbf{A}\) zu ihrer eigenen Transponierten addiert, dann ist das Ergebnis eine symmetrische Matrix. In Formeln notieren wir Folgendes: Wenn \(\mathbf{A}\) eine quadratische Matrix ist, dann ist \(\mathbf{A}+\mathbf{A}^{T}\) eine symmetrische Matrix.
Dass diese Aussage wahr ist, können wir folgendermaßen zeigen. Wir starten mit dem Ausdruck \((\mathbf{A}+\mathbf{A}^{T})^{T}\) und vereinfachen ihn gemäß der obigen Rechenregeln:
Das ist aber genau die Eigenschaft, die eine quadratische Matrix zu einer symmetrischen Matrix macht.
Analog dazu können wir zeigen, dass \(\mathbf{A} - \mathbf{A}^{T}\) eine antisymmetrische Matrix ist:
Wir wissen also, dass \(\mathbf{A}+\mathbf{A}^{T}\) eine symmetrische Matrix und \(\mathbf{A}-\mathbf{A}^{T}\) eine antisymmetrische Matrix ist. Addieren wir die beiden, erhalten wir
Teilen wir auf beiden Seiten der Gleichung durch 2 erhalten wir
und haben so die quadratische Matrix \(\mathbf{A}\) in eine symmetrischen und einen antisymmetrischen Teil zerlegt.
Zusammenfassung und Ausblick#
In diesem Kapitel haben wir symmetrische Matrizen kennengelernt, die sich beim Transponieren nicht verändern. Symmetrische Matrizen sind eines der wichtigsten Hilfsmittel der Linearen Algebra und werden uns aber auch in der Analysis wieder begegnen, wenn es um die Bestimmung von Extrema zweidimensionaler reellwertiger Funktionen gehen wird.
