12.6 Wendepunkte#
Auch die Nullstellen der zweiten Ableitung haben eine besondere geometrische Bedeutung, die wir in diesem Kapitel uns erarbeiten.
Lernziele#
Lernziele
Sie wissen, was ein Wendepunkt ist.
Sie kennen die Bedingungen, unter denen eine Funktion einen Wendepunkt hat.
Sie wissen, was ein Sattelpunkt/Terassenpunkt ist.
Wendepunkt#
In der Mathematik nennt man einen Punkt, an dem sich das Krümmungsverhalten einer Funktion ändert, Wendepunkt. In dem folgenden Beispiel geht der Funktionsgraph bei \(W\) von einer Rechtskrümmung in eine Linkskrümmung über.
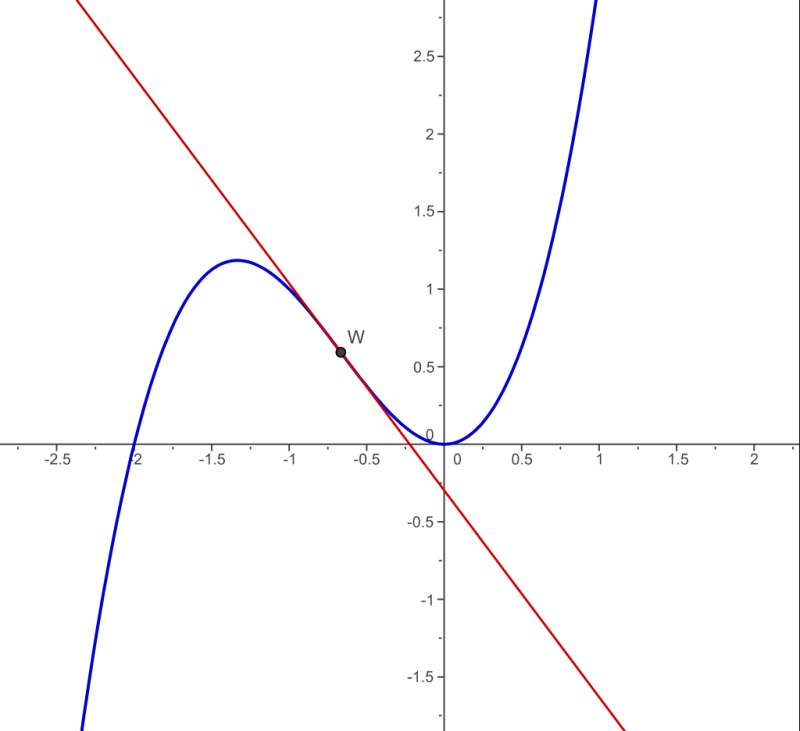
Fig. 24 Quelle: Wolfgang Dvorak - Eigenes Werk, CC BY-SA 3.0, https://commons.wikimedia.org/w/index.php?curid=1283725#
Ist eine Funktion zweimal differenzierbar, dann hat die erste Ableitung bei einem Wendepunkt ein lokales Maximum oder ein lokales Minimum. Es ist also notwendig, dass die zweite Ableitung an einer Wendestelle Null ist:
Damit eine Stelle \(x_0\) hinreichend eine Wendestelle ist, muss die zweite Ableitung auf einen Vorzeichenwechsel untersucht werden oder die dritte Ableitung überprüft werden. Liegt ein Vorzeichenwechsel von \(f''\) an der Stelle \(x_0\) von Minus nach Plus vor, dann liegt eine Rechts-links-Wendestelle vor. Alternativ besagt \(f'''(x_0) > 0\), dass eine Rechts-links-Wendestelle vorliegt. Liegt ein Vorzeichenwechsel von \(f''\) von Plus nach Minus vor oder ist \(f'''(x_0)<0\), dann liegt eine Links-rechts-Wendestelle vor.
Sattelpunkt#
Manchmal hat eine Wendestelle auch gleichzeitig eine Tangente mit Steigung Null, d.h. einer Tangente die parallel zur x-Achse ist. Dann nennt man diesen Punkt Sattelpunkt oder Terrassenpunkt. Die folgende Abbildung zeigt ein Beispiel mit zwei Sattelpunkten.
Fig. 25 Quelle: HilberTraum - Eigenes Werk, CC BY-SA 4.0, https://commons.wikimedia.org/w/index.php?curid=34972980#
Video “Wendestellen und Sattelstellen” von Mathematische Methoden
Zusammenfassung und Ausblick#
Die Analyse der wichtigsten geometrischen Eigenschaften einr Funktion werden auch Kurvendiskussion genannt.
