9.6 Unstetigkeitsstellen

Vielleicht mag es verwundern, dass wir dem Thema Unstetigkeit ein eigenes Thema widmen. In diesem Kapitel geht es aber nicht nur darum festzuhalten, was Unstetigkeit bedeutet, sondern vor allem darum, die Art der Unstetigkeit zu klassifizieren.

Lernziele

Lernziele

• Sie kennen hebbare Unstetigkeitsstellen und können sie korrigieren.

• Sie kennen Unstetigkeitsstellen 1. Art, d.h. Funktionen mit Sprungsstellen.

• Sie kennen Unstetigkeitsstellen 2. Art, d.h. Funktionen mit einer Polstelle oder einer Oszillation.

Hebbare Unstetigkeitsstellen

Bei hebbaren Unstetigkeitsstellen gibt es den linksseitigen Grenzwert und den rechtsseitigen Grenzwert und diese stimmen sogar überein. Aber die beiden Grenzwerte sind nicht gleich dem Funktionswert oder aber die Funktion hat an dieser Stelle eine Definitionslücke.

Als Beispiel betrachten wir die Funktion

\[f(x) = \frac{x^2-1}{x-1}.\]

Da der Nenner bei \(x_0 = 1\) Null wird, ist diese Funktion an der Stelle \(x_0 = 1\) nicht definiert, der Funktionswert \(f(1)\) existiert nicht. Wir berechnen nun den linksseitigen Grenzwert:

\[\lim_{x\to 1^{-}} \left(\frac{x^2-1}{x-1}\right) = \lim_{x\to 1^{-}}\left(\frac{(x+1)(x-1)}{x-1}\right) = \lim_{x\to 1^{-}}(x + 1) = 2.\]

Aber Das Kürzen des Bruches ist erlaubt, da wir uns von links der Stelle \(x_0 = 1\) nähern und daher immer \(x \neq 1\) gilt. Analog dazu berechnen wir den rechtsseitigen Grenzwert als

\[\lim_{x\to 1^{+}} \left(\frac{x^2-1}{x-1}\right) = \lim_{x\to 1^{+}}(x + 1) = 2,\]

wo erneut das Kürzen erlaubt ist, weil wir uns von rechts der Stelle \(x_0 = 1\) nähern und daher stets \(x\neq 1\) gilt. Wir führen jetzt eine neue Funktion \(\tilde{f}\) ein, die folgendermaßen definiert ist:

\[\begin{split}\tilde{f}(x) = \begin{cases} \frac{x^2-1}{x-1}, \quad & x\neq 1, \\ 2, \quad & x = 1. \end{cases}\end{split}\]

Die neue Funktion \(\tilde{f}\) behebt die Lücke bzw. die Unstetigkeitsstelle.

Sprungstellen

Wenn eine Funktion an der Stelle \(x_0\) einen linksseitigen und einen rechtsseitigen Grenzwert hat, diese jedoch unterschiedlich sind, liegt eine sogenannte Sprungstelle vor.

Als Beispiel betrachten wir die sogenannte Sägezahnfunktion, die in der Signalverarbeitung häufig verwendet wird. Auf der x-Achse ist die Zeit in Sekunden abgebildet. Für 2 Sekunden wachsen die Funktionswerte linear von -1 auf 1, dann springen die Funktionswerte zurück auf -1, um dann erneut in 2 Sekunden wieder auf 1 linear anzuwachsen. Dieser Vorgang wiederholt sich periodisch alle 2 Sekunden.

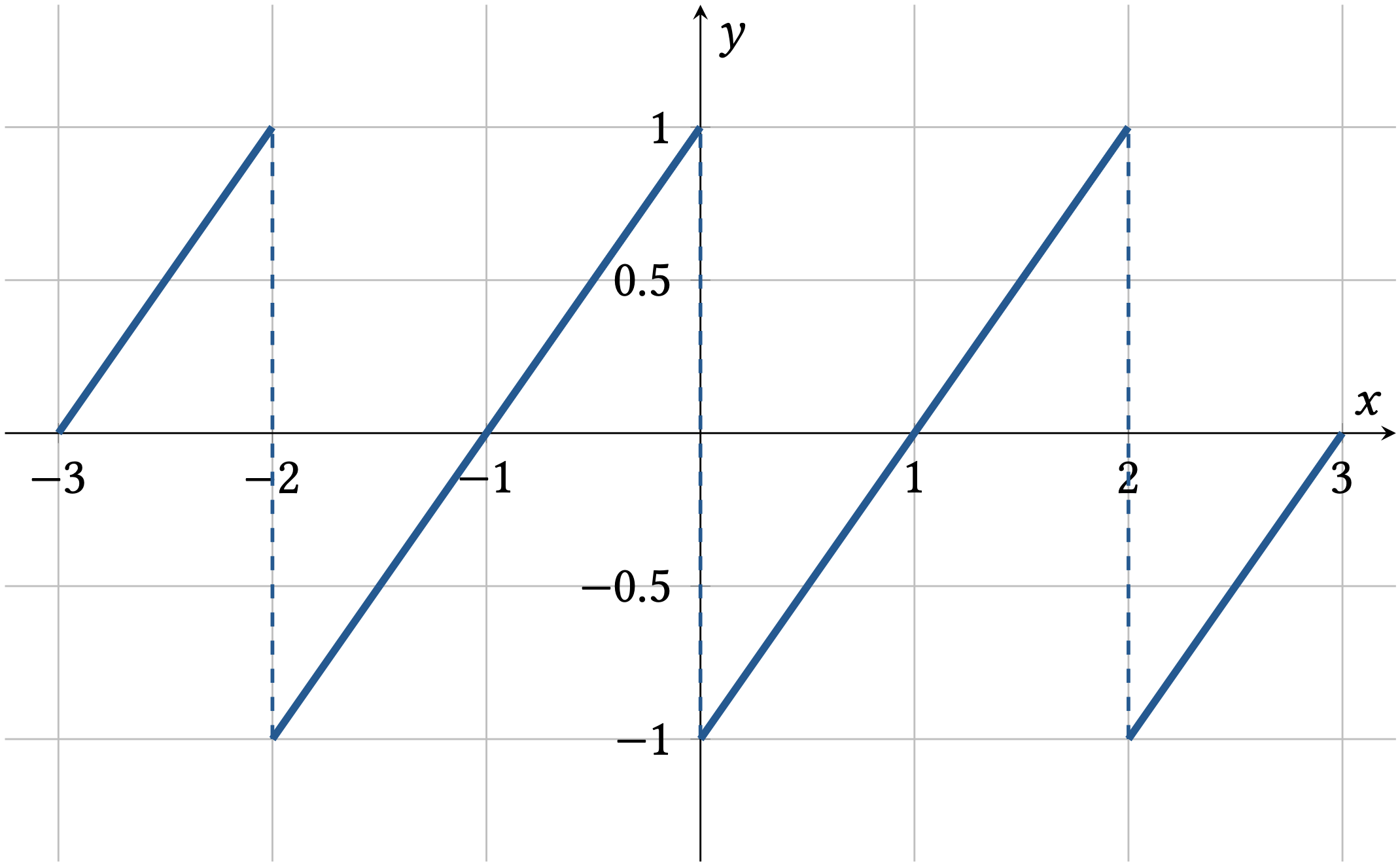
Fig. 19 Beispiel einer Sägezahnfunktion, die zwischen \(-1\) und \(1\) oszilliert und die Periode \(T = 2\) hat

Betrachten wir nun beispielsweise die Stelle \(x_0 = 0\), so stellen wir fest, dass der linksseitige Grenzwert

\[\lim_{x\to 0^{-}}f(x) = 1\]

ist, während der rechtsseitige Grenzwert

\[\lim_{x\to 0^{+}}f(x) = -1\]

ist. Diese Stelle ist daher eine Sprungstelle (so wie auch alle weiteren Vielfachen von 2).

Polstellen

Hebbare Unstetigkeitsstellen und Sprungstellen werden auch als Unstetigkeitsstellen 1. Art bezeichnet. Nun widmen wir uns noch den Unstetigkeitsstellen 2. Art. Dazu gehören die Stellen, an denen überhaupt kein Grenzwert existiert. Aber auch die Stellen, an denen der Grenzwert nur im uneigentlichen Sinne existiert, gehören dazu.

Eine Definitionslücke einer reellen Funktion, bei der die Funktionswerte in der Umgebung betragsmäßig beliebig groß werden, nennen wir Polstelle, also wenn beispielsweise

\[\lim_{x\to x_0}f(x)=+\infty \; \text{ oder } \; \lim_{x\to x_0}f(x) = -\infty.\]

Beispielsweise hat die Funktion

\[f(x) = \frac{1}{(x-1)^2}, \quad x\neq 1\]

an der Stelle \(x_0 = 1\) eine Polstelle, wie auch die folgende Visualisierung zeigt:

Fig. 20 Beispiel einer Funktion mit einer Polstelle bei \(x_0 = 1\)

Video “Unstetigkeitsstellen bestimmen” von MathePeter

Zusammenfassung und Ausblick

In diesem Kapitel haben wir die verschiedenen Arten von Unstetigkeitsstellen erläutert. Im nächsten Kapitel steigen wir in das Thema Ableitungen ein.