5.6 Winkel#
Schneiden sich Gerade und Gerade oder Gerade und Ebene in einem Schnittpunkt bzw. Ebene und Ebene in einer Schnittgeraden, ist die Frage interessant, welchen Winkel diese Objekte zueinander einnehmen. In diesem Kapitel werden wir uns mit diesen drei Fällen beschäftigen und die dazugehörigen Winkel berechnen.
Lernziele#
Lernziele
Sie können den Winkel zwischen zwei Geraden berechnen.
Sie können den Winkel zwischen einer Gerade und einer Ebene berechnen.
Sie können den Winkel zwischen zwei Ebenen berechnen.
Winkel zwischen zwei Geraden#
Schneiden sich zwei Geraden \(g_1\) und \(g_2\) in einem Schnittpunkt, treten zwei verschiedene Winkel auf. Hier in der Skizze sind diese mit \(\alpha\) und \(\beta\) gekennzeichnet.
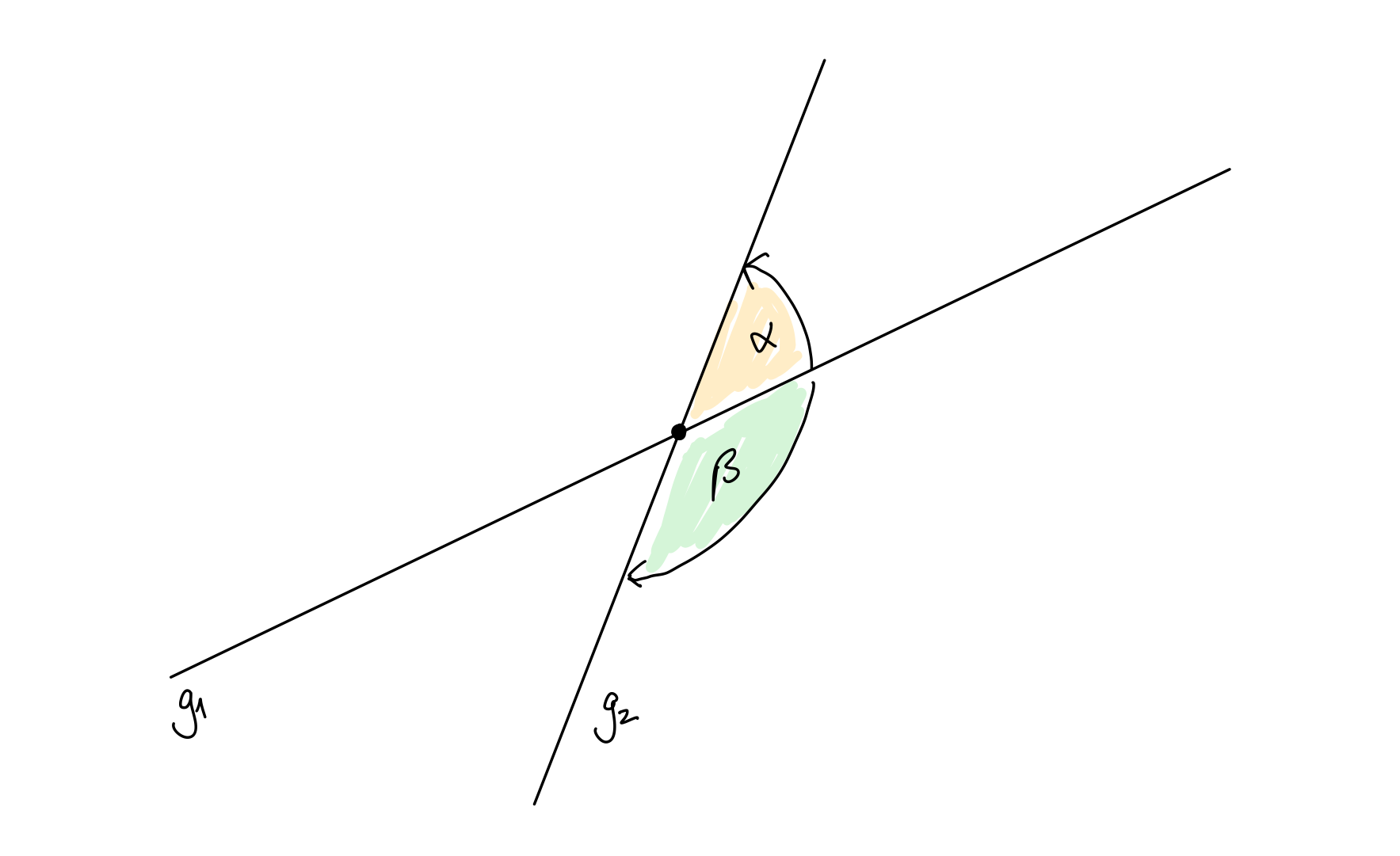
Fig. 15 Winkel zwischen zwei Geraden; Quelle: eigene Darstellung; Lizenz: CC BY-SA 4.0#
Als Schnittwinkel zweier Geraden mit dem mathematischen Symbol \(\angle(g_1,g_2)\) definieren wir den kleineren der beiden Winkel. Um den Schnittwinkel zu berechnen, können wir den Winkel zwischen den beiden Richtungsvektoren der Geraden berechnen. Ist die erste Geradengleichung gegeben als \(g_1: X = P_1 + s\cdot\vec{v_1}\) und die zweite Geradengleichung als \(g_2: X = P_2 + t\cdot\vec{v_2}\), dann können wir die geometrische Interpretation des Skalarproduktes nutzen:
Dabei ist \(\varphi=\angle(\vec{v_1},\vec{v_2})\) der zwischen den beiden Richtungsvektoren \(\vec{v_1}\) und \(\vec{v_2}\) eingeschlossene Winkel. Ist das Skalarprodukt positiv, ist der Winkel spitz und entspricht dem kleineren Winkel, also dem gesuchten Schnittwinkel. Ist das Skalarprodukt negativ, haben wir den stumpfen Winkel. Um diese Fallunterscheidung zu umgehen, bilden wir zuerst den Betrag des Skalarproduktes und können dann die Umkehrfunktion Arkuskosinus nutzen. Damit lautet die Formel zur Berechnung des Schnittwinkels \(\angle(g_1,g_2)\):
Video “Winkel zwischen zwei Geraden” von Cornelsen
Video “Schnittpunkt und Schnittwinkel berechnen” von MathePeter
Übung “Winkel Geraden” von Mathebattle
Winkel zwischen Gerade und Ebene#
Möchten wir den Winkel zwischen einer Gerade und einer Ebene berechnen, nehmen wir den Richtungsvektor der Geraden und den Normalenvektor der Ebene. Angenommen, die Geradengleichung lautet \(g: X = P + s\cdot\vec{v}\) und ein Normalenvektor der Ebene ist \(\vec{n}\). Der gesuchte Schnittwinkel zwischen der Gerade und der Ebene soll \(\varphi\) heißen. Dann wissen wir, dass der Winkel zwischen dem Normalenvektor und dem Richungsvektor der Geraden gerade \(90^{\circ}-\varphi\) ist. Um uns erneut Fallunterscheidungen zwischen spitzen und stumpfen Winkel zu ersparen, nehmen wir auch hier den Betrag des Skalarproduktes:
Wir könnten nun erneut den Arkuskosinus anwenden und dann die entstehende Gleichung nach dem gesuchten Schnittwinkel \(\varphi\) auflösen. Da aber \(\cos(90^{\circ}-\varphi)=\sin(\varphi)\) gilt, können wir auch direkt den Schnittwinkel über die Formel
berechnen.
Video “Winkel zwischen Gerade und Ebene” von Mathematrick
Video “Winkel Gerade - Ebene” von MathePeter
Übung “Winkel Gerade - Ebene” von Mathebattle
Winkel zwischen Ebene und Ebene#
Soll der Schnittwinkel zweier Ebenen berechnet werden, werden von beiden Ebenen Normalenvektoren genommen. \(\vec{n_1}\) bezeichne einen Normalenvektor der ersten Ebene und \(\vec{n_2}\) einen Normalenvektor der zweiten Ebene. Dann gilt wiederum für den Schnittwinkel
Video “Schnittwinkel” von Flip the Classroom
Video “Winkel zwischen zwei Ebenen” von Mathematrick
Video “Winkel Ebene - Ebene” von MathePeter
Übung “Winkel Ebenen” von Mathebattle
Zusammenfassung und Ausblick#
Mit der Berechnung der Schnittwinkel schließen wir das Thema Punkte, Geraden und Ebenen ab. Als nächstes werden wir uns mit Matrizen beschäftigen.
