4.3 Geometrische Interpretation Skalarprodukt

4.3 Geometrische Interpretation Skalarprodukt#

In diesem Kapitel werden wir das Skalarprodukt für Vektoren in der Geometrie anwenden. Wir setzen ein kartesisches, dreidimensionales Koordinatensystem voraus und stellen Verschiebungen bzw. Bewegungen bzgl. dieses Koordinatensystems als Vektoren des Standardvektorraumes \(\mathbb{R}^3\) dar.

Lernziele#

Lernziele

Sie kennen den Zusammenhang zwischen Skalarprodukt und Betrag/Länge eines Vektors:

\[|\vec{a}|=\sqrt{\vec{a}\cdot\vec{a}}.\]
Sie wissen, welche Bedeutung das Skalarprodukt zweier Vektoren geometrisch hat: Das Skalarprodukt der Vektoren \(\vec{a}\) und \(\vec{b}\) ist das Produkt aus den Längen der beiden Vektoren und dem Kosinus des von den beiden Vektoren eingeschlossenen Winkels \(\varphi = \angle (\vec{a},\vec{b})\):

\[\vec{a}\cdot\vec{b} = |\vec{a}|\cdot|\vec{b}| \cdot \cos(\varphi).\]
Sie können den Winkel zwischen zwei Vektoren berechnen, wenn Sie das Skalarprodukt und die beiden Längen kennen:

\[\varphi = \arccos\left(\frac{\vec{a}\cdot\vec{b}}{|\vec{a}|\cdot|\vec{b}|}\right), \quad \vec{a}\neq\vec{0}, \vec{b}\neq\vec{0}.\]

Skalarprodukt und Betrag/Länge von Vektoren#

Für Vektoren des reellen Standardvektorraumes \(\vec{a}\in\mathbb{R}^n\) ist der Betrag des Vektors definiert als

\[|\vec{a}| = \sqrt{a_1^2 + a_2^2 + \ldots + a_n^2}.\]

Im geometrischen Kontext wird oft der Begriff »Länge eines Vektors« anstatt »Betrag eines Vektors« verwendet. Das liegt an der Interpretation des geometrischen Vektors als Verschiebung. Ist ein Vektor \(\vec{v}\in\mathbb{R}^3\) gegeben und ist \(P\) ein beliebiger Punkt in einem kartesischen 3D-Koordinatensystem, dann führt die Verschiebung \(\vec{v}\) zu einem neuen Punkt \(Q\), also \(P = \vec{v} = Q\). Die Länge der Strecke zwischen den Punkten \(P\) und \(Q\) ist gleich dem Betrag des Vektors \(\vec{v}\), also

\[\overline{PQ} = \sqrt{v_1^2 + v_2^2 + v_3^2} = |\vec{v}|.\]

Wenn wir jetzt das Skalarprodukt von \(\vec{v}\) mit sich selbst berechnen, erhalten wir

\[\begin{split}\vec{v}\cdot\vec{v} = \begin{pmatrix} v_1 \\ v_2 \\ v_3 \end{pmatrix} \cdot \begin{pmatrix} v_1 \\ v_2 \\ v_3 \end{pmatrix} = v_1^2 + v_2^2 + v_3^2.\end{split}\]

Das ist genau der Ausdruck, der beim Betrag bzw. der Länge des Vektors unter der Wurzel steht. Wir können also auch das Skalarprodukt eines Vektors mit sich selbst nutzen, um den Betrag bzw. die Länge des Vektors zu berechnen:

\[|\vec{v}|=\sqrt{\vec{v}\cdot\vec{v}}.\]

Alternativ können wir auch die Formel

\[|\vec{v}|^2 = \vec{v}\cdot\vec{v}\]

nutzen.

Skalarprodukt und eingeschlossener Winkel#

Als nächstes führen wir den eingeschlossenen Winkel zwischen zwei Vektoren ein. Geometrisch interpretieren wir die beiden Vektoren \(\vec{a}\in\mathbb{R}^3\) und \(\vec{b}\in\mathbb{R}^3\) als Verschiebungen, die beide an einem gemeinsamen Punkt starten. Unabhängig von der Reihenfolge der Vektoren wird der kleinere Winkel zwischen den beiden Vektoren \(\vec{a}\) und \(\vec{b}\) als eingeschlossener Winkel bezeichnet. Er liegt somit zwischen 0 und 180° (Gradmaß) bzw. zwischen 0 und \(\pi\) (Bogenmaß). Wir verwenden für den eingeschlossenen Winkel das Symbol \(\angle (\vec{a},\vec{b})\) oder den griechischen Buchstaben Phi \(\varphi\).

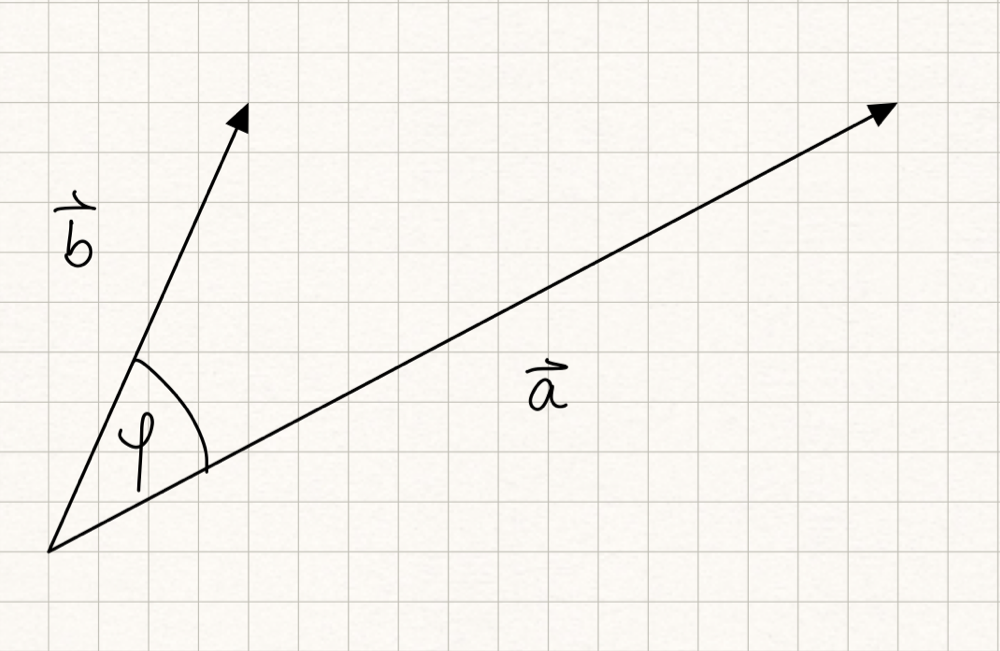
../_images/eingeschlossener_winkel.png — Fig. 10 Eingeschlossener Winkel \(\varphi = \angle (\vec{a},\vec{b})\) zwischen den Vektoren \(\vec{a}\) und \(\vec{b}\); Quelle: eigene Darstellung, Lizenz: CC BY-SA 4.0#

Wenn die beiden Vektoren \(\vec{a}\) und \(\vec{b}\) die gleiche Richtung haben, ist \(\varphi = 0^{\circ}\) (bzw. \(\varphi=0\) im Bogenmaß). Falls sie die entgegengesetzte Richtung haben, gilt für den eingeschlossenen Winkel \(\varphi = 180^{\circ}\) (bzw. \(\varphi = \pi\) im Bogenmaß).

Als nächstes führen wir noch einen Vektor \(\vec{c}\) als Differenz der beiden Vektoren \(\vec{a}\) und \(\vec{b}\) ein, also

\[\vec{c} = \vec{b} - \vec{a}.\]

Da \(\vec{a} + \vec{b} + \vec{c} = \vec{a} + \vec{b} + (\vec{b}-\vec{a}) = \vec{0}\) der Nullvektor ist, liegt ein Polygonzug bzw. eine Vektorkette vor. Die drei Vektoren sind die gerichteten Seiten eines Dreiecks, wie die folgende Abbildung zeigt.

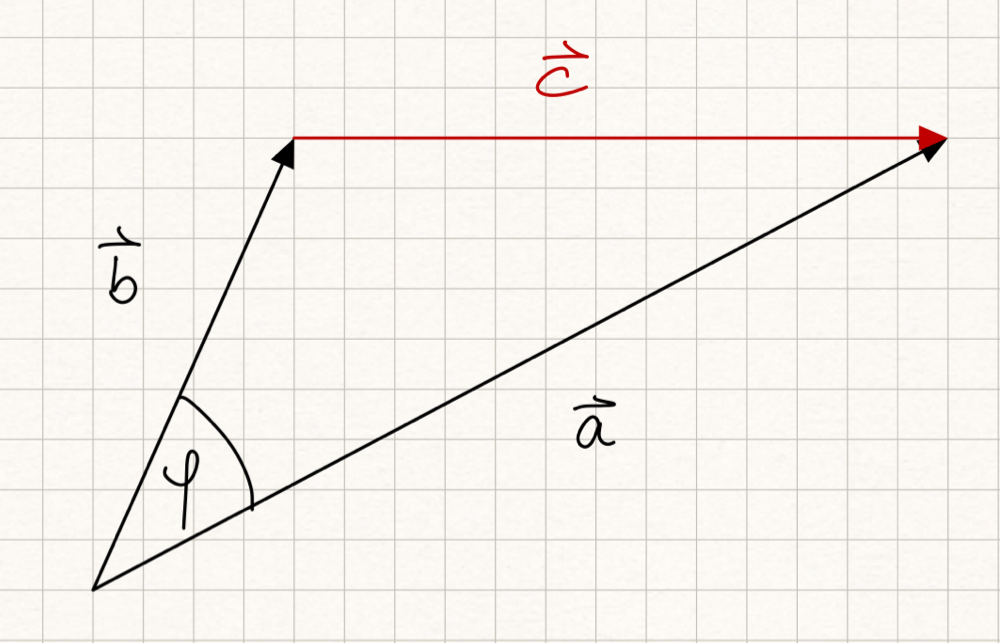
../_images/kosinussatz.png — Fig. 11 Kosinussatz; Quelle: eigene Darstellung, Lizenz: CC BY-SA 4.0#

Für das Dreieck gilt der Kosinussatz:

(1)#\[|\vec{c}|^2 = |\vec{a}|^2 + |\vec{b}|^2 - 2\cdot |\vec{a}| \cdot |\vec{b}|\cdot\cos(\varphi).\]

Da aber \(\vec{c} = \vec{a} - \vec{b}\) gilt, können wir mit Hilfe der 2. binomischen Formel den Term \(|\vec{c}|^2\) durch das Skalarprodukt von \((\vec{a}-\vec{b})\) mit sich selbst ersetzen:

\[\begin{align*} |\vec{c}|^2 &= |\vec{a}-\vec{b}|^2 = \\ &= (\vec{a}-\vec{b}) \cdot (\vec{a}-\vec{b}) = \\ &= \vec{a}\cdot\vec{a} - 2\cdot\vec{a}\cdot\vec{b} + \vec{b}\cdot\vec{b}. \end{align*}\]

Letzteres setzen wir nun auf der linken Seite von Gleichung (1) ein:

\[\vec{a}\cdot\vec{a} - 2\cdot\vec{a}\cdot\vec{b} + \vec{b}\cdot\vec{b} = |\vec{a}|^2 + |\vec{b}|^2 - 2\cdot |\vec{a}| \cdot |\vec{b}|\cdot\cos(\varphi).\]

Jetzt können wir ausnutzen, dass \(\vec{a}\cdot\vec{a} = |\vec{a}|^2\) gilt und \(\vec{b}\cdot\vec{b} = |\vec{b}|^2\) und die Terme auf beiden Seiten der Gleichung subtrahieren. Es bleibt die Gleichung

\[- 2\cdot\vec{a}\cdot\vec{b} = - 2\cdot |\vec{a}| \cdot |\vec{b}|\cdot\cos(\varphi)\]

übrig. Zuletzt teilen wir noch auf beiden Seiten durch \((-2)\) und erhalten

\[\vec{a}\cdot\vec{b} = |\vec{a}|\cdot|\vec{b}| \cdot \cos(\varphi).\]

Das ist die geometrische Interpretation des Skalarproduktes im \(\mathbb{R}^3\).

Was ist die geometrische Interpretation des Skalarproduktes?

Im \(\mathbb{R}^3\) kann das Skalarprodukt der beiden Vektoren \(\vec{a}\in\mathbb{R}^3\) und \(\vec{b}\in\mathbb{R}^3\) über die Längen der Vektoren und den eingeschlossenen Winkel \(\varphi = \angle (\vec{a}, \vec{b})\) gemäß der Formel

\[\vec{a}\cdot\vec{b} = |\vec{a}|\cdot|\vec{b}| \cdot \cos(\varphi)\]

berechnet werden.

Winkelberechnungen mit dem Skalarprodukt#

Das Skalarprodukt der Vektoren \(\vec{a}\) und \(\vec{b}\) kann über die Beträge/Längen der Vektoren \(|\vec{a}|\) und \(|\vec{b}|\) sowie dem Kosinus-Wert des eingeschlossenen Winkels \(\varphi = \angle (\vec{a},\vec{b})\) berechnet werden. Sofern die beiden Vektoren \(\vec{a}\) und \(\vec{b}\) nicht der Nullvektor sind, also \(\vec{a}\neq\vec{0}\) bzw. \(\vec{b}\neq\vec{0}\) gelten, können wir die obige Formel auch umkehren. Aus dem Skalarprodukt kann dann mit Hilfe der Arkuskosinus-Funktion der Winkel \(\varphi\) berechnet werden:

\[\varphi = \arccos\left(\frac{\vec{a}\cdot\vec{b}}{|\vec{a}|\cdot|\vec{b}|}\right), \quad \vec{a}\neq\vec{0}, \vec{b}\neq\vec{0}. \]

Mini-Übung

Gehen Sie auf die Seite https://o-mathe.de/analytische-geometrie/skalarprodukt/skalarprodukt/untersuchungen/lernstrecke und machen Sie Aufgabe 1.

Aus dieser Beziehung können einige Schlussfolgerungen gezogen werden, die wir auch im nächsten Kapitel erneut aufgreifen und vertiefen werden.

Sind \(\vec{a}\) und \(\vec{b}\) parallel, ist also der eingeschlossene Winkel \(\varphi = 0\), dann gilt

\[\vec{a}\cdot\vec{b} = |\vec{a}| \cdot |\vec{b}|.\]
Sind \(\vec{a}\) und \(\vec{b}\) antiparallel, gilt also für den eingeschlossenen Winkel \(\varphi = \pi\), dann gilt

\[\vec{a}\cdot\vec{b} = - |\vec{a}| \cdot |\vec{b}|.\]
Sind die beiden Vektoren \(\vec{a}\) und \(\vec{b}\) orthogonal (stehen senkrecht aufeinander), dann gilt

\[\vec{a}\cdot\vec{b} = 0.\]
Ist \(\varphi\) ein spitzer Winkel, so gilt

\[\vec{a}\cdot\vec{b} > 0.\]
Ist \(\varphi\) ein stumpfer Winkel, so gilt

\[\vec{a}\cdot\vec{b} < 0.\]

Die große Bedeutung des Skalarproduktes in der Geometrie erkennen Sie daran, dass es sehr viele Erklärvideos zu diesem Thema gibt. Einige Videos zu dem Thema sind im Folgenden gelistet.

Zusammenfassung und Ausblick#

In diesem Kapitel haben wir die geometrische Interpretation des Skalarproduktes kennengelernt. Einige Autoren von Mathematikbüchern gehen den umgekehrten Weg und definieren das Skalarprodukt über die Formel \(\vec{a}\cdot\vec{b} = |\vec{a}|\cdot|\vec{b}| \cdot \cos(\varphi)\). Im nächsten Kapitel werden wir die Anwendungen des Skalarproduktes in der Geometrie (und damit in Physik und Technische Mechanik) weiter vertiefen.