5.1 Periodische Funktionen#
In diesem Kapitel werden wir uns mit periodischen Funktionen beschäftigen. Insbesondere im Maschinenbau finden sich zahlreiche Anwendungen von periodischen Funktionen, z.B. in der Technischen Mechanik oder in der Regelungstechnik. Viele mechanische Systeme, wie z.B. Federsysteme, Pendel oder rotierende Wellen, führen periodische Schwingungen aus. Auch in der Regelungstechnik werden periodische Steuergrößen erzeugt, die zur Regelung von Systemen verwendet werden. Beispiele sind periodische Signale, wie z.B. Rechteck-, Dreieck- oder Sinusfunktionen. Diese Signale werden verwendet, um elektrische, mechanische oder hydraulische Systeme zu steuern.
Lernziele#
Lernziele
Sie können erklären, was eine periodische Funktion ist.
Sie können Beispiele von periodischen Funktionen nennen wie
Sinus- und Kosinusfunktion,
Rechteckfunktion,
Dreiecksfunktion und
Sägezahnfunktion.
Periodische Funktionen - was ist das?#
Bei einer periodischen Funktion wiederholen sich in regelmäßigen Abständen die Funktionswerte wieder. Der Abstand, nachdem sich die Funktionswerte beginnen zu wiederholen, heißt Periodendauer.
Was ist … eine periodische Funktion?
Eine Funktion heißt periodisch, wenn sich die Funktionswerte regelmäßig wiederholen. Als mathematische Formel ausgedrückt ist eine Funktion \(f\) periodisch mit der Periode \(p\), wenn gilt:
Video “Periodische Funktion” von lernflix
Beispiele periodischer Funktionen#
Sinus- und Kosinusfunktion#
Sinus und Kosinus sind die beiden wichtigsten periodischen Funktionen. Sie werden auch dazu genutzt, um andere periodische Funktionen zu approximieren (Stichwort: Fourierreihe). Beide haben eine Periode von \(2\pi\).
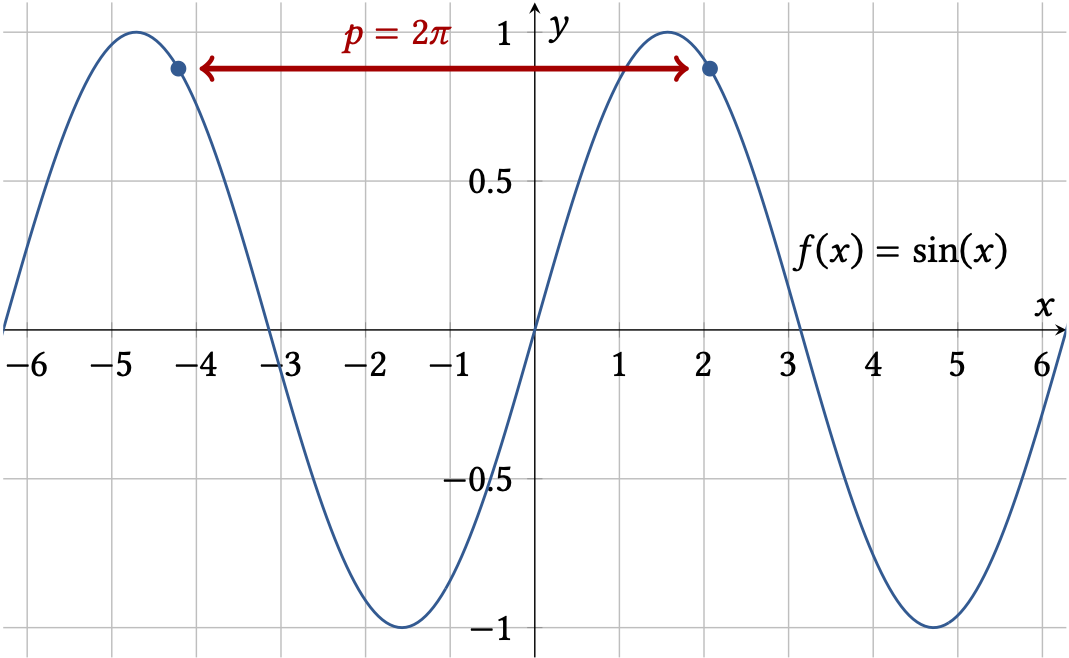
Fig. 2 Sinusfunktion mit einer Periode \(p = 2\pi\)#
Wir werden in den nächsten Kapiteln die Sinus- und Kosinusfunktionen modifizieren. Im folgenden Video werden verschiedene Möglichkeiten vorgestellt, um die Sinusfunktion zu transformieren. Für die Kosinusfunktion gelten die gleichen Transformationen analog.
Video “Sinusfunktion Transformation” von Daniel Jung
Rechteckfunktion#
Die Rechteckfunktion ist zunächst einmal keine periodische Funktion. Als erstes werden eine Periode \(T\) und eine Konstante \(c\) festgelegt. Dann wird die Rechteckfunktion definiert als die Funktion, deren Funktionswerte im Intervall \([-\frac{T}{2}, \frac{T}{2}]\) gleich der Konstante \(c\) sind. Und außerhalb dieses Intervalls sollen die Funktionswerte 0 sein (übrigens, manchmal wird auch ein anderer Wert als 0 genommen). Mathematisch wird das folgendermaßen ausgedrückt:
Der Funktionsgraph der Rechteckfunktion sieht folgendermaßen aus:
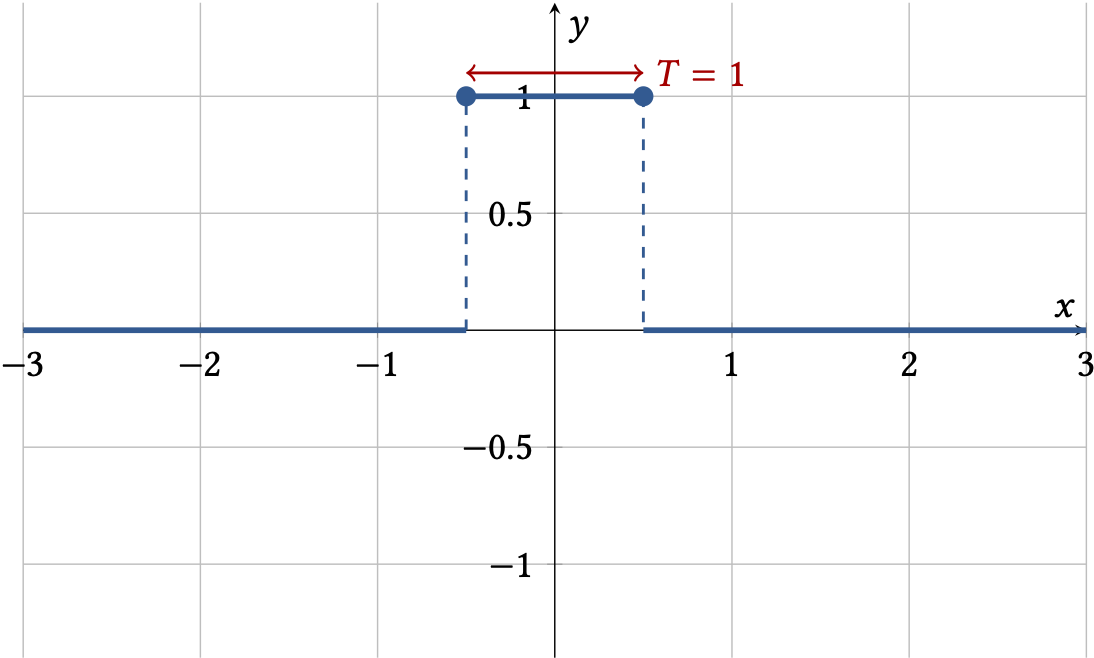
Fig. 3 Beispiel einer Rechteckfunktion: Periode \(T = 1\) und \(c = 1\)#
Jetzt wird die Periode von \(0\) bis \(T\) gelb markiert.
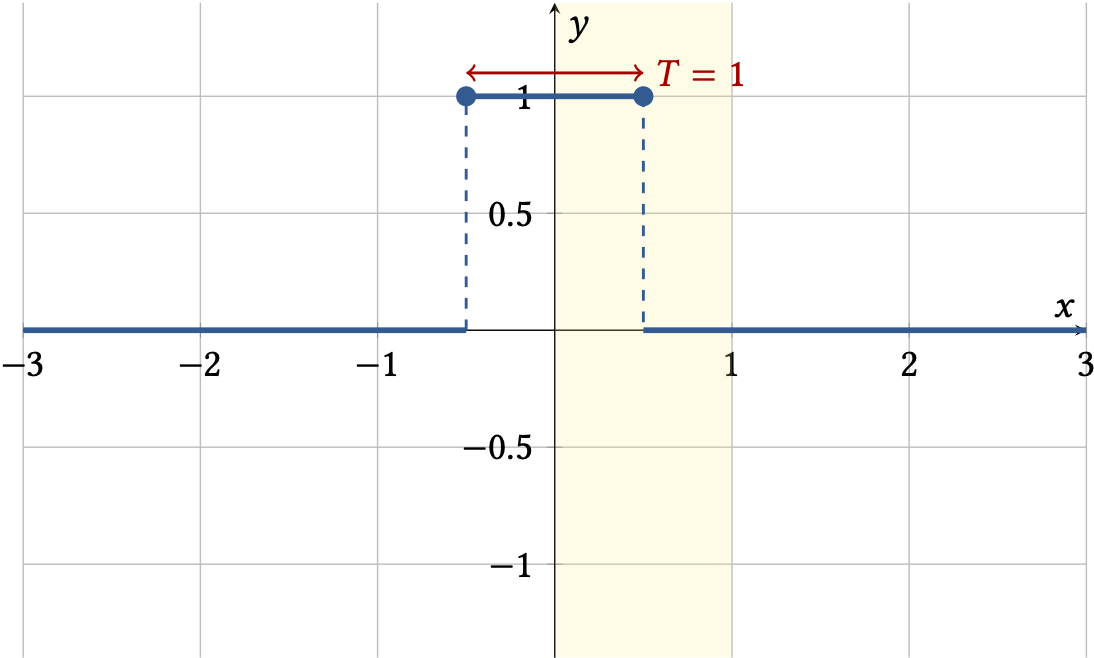
Fig. 4 Beispiel einer Rechteckfunktion: das Periodenintervall \([0,T]\) ist gelb markiert#
Als letztes wird der Funktionsgraph periodisch wiederholt. Damit ist gemeint, dass das gelb markierte Gebiet links und rechts immer wieder angefügt wird. Dadurch entsteht eine neue Funktion, deren Funktionsgraph in der nächsten Abbildung zu sehen ist.
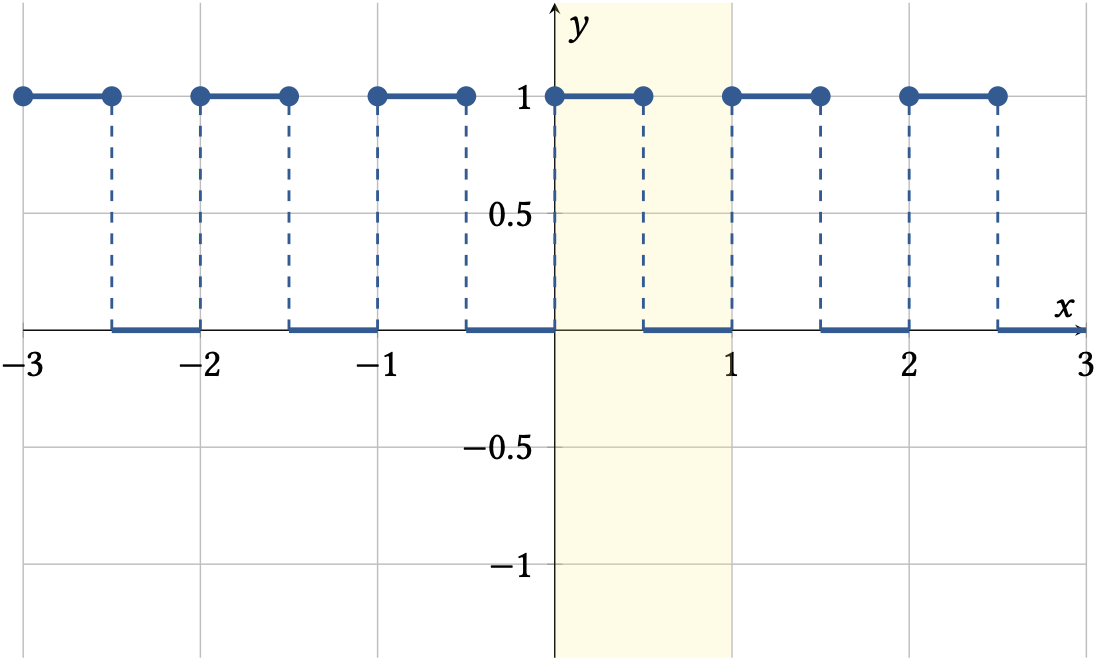
Fig. 5 Beispiel einer Rechteckfunktion, die periodisch fortgesetzt wurde#
Diese neue Funktion ist nun eine periodische Funktion. Sie wird häufig in der Signalverarbeitung verwendet. Beispielsweise dient sie als Taktsignal für digitale Prozessoren und Controller.
Dreiecksfunktion#
Die Dreiecksfunktion ist eine periodische Funktion, die ebenfalls in der Signalverarbeitung häufig vorkommt. Sie hat eine Periode \(T\) und oszilliert zwischen zwei Werten \(c_1\) und \(c_2\), wobei der Anstieg von \(c_1\) auf \(c_2\) und der Abfall von \(c_2\) auf \(c_1\) jeweils linear ist.
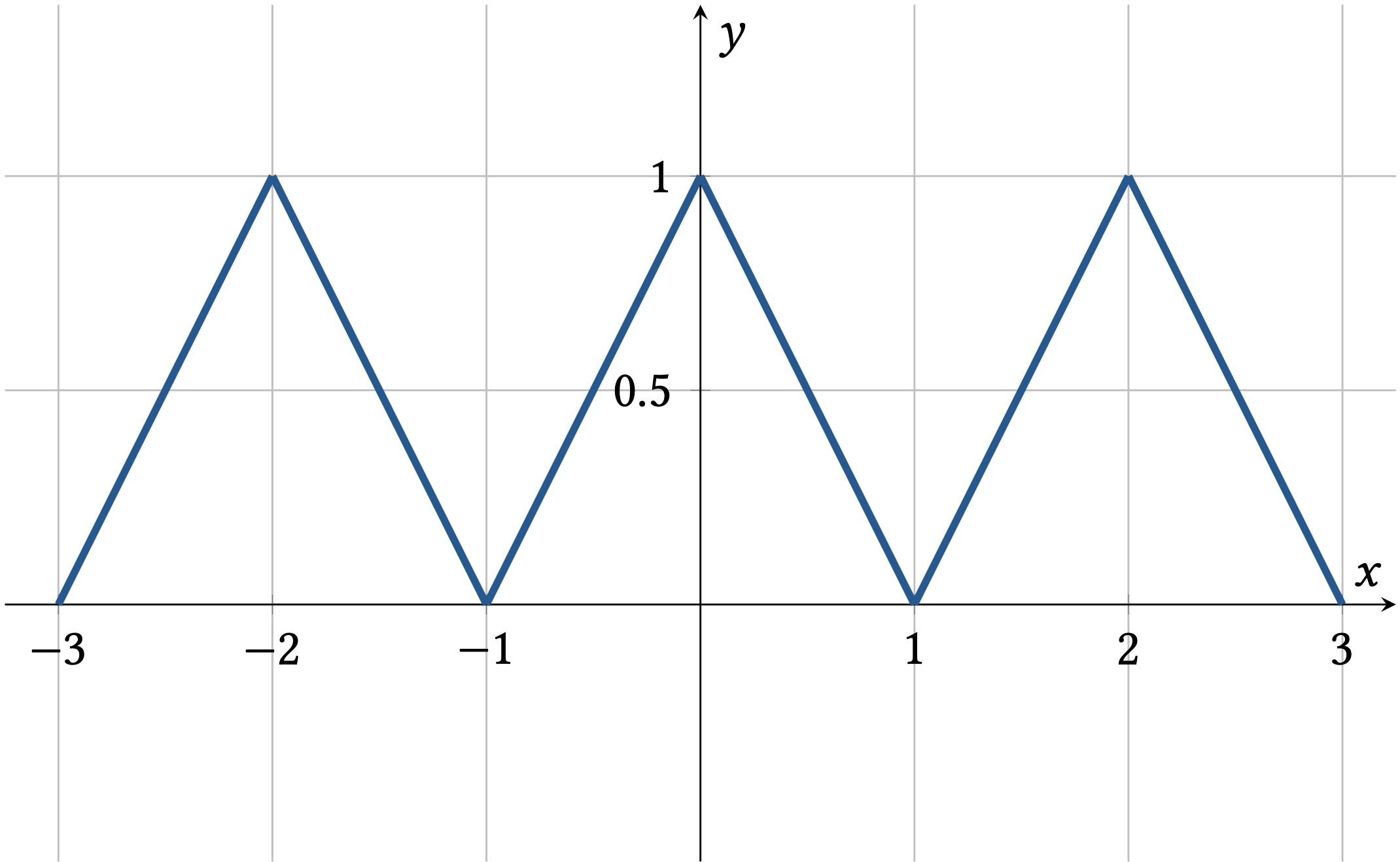
Fig. 6 Beispiel einer Dreiecksfunktion, die zwischen \(0\) und \(1\) oszilliert und die Periode \(T = 2\) hat#
Sägezahnfunktion#
Die Sägezahnfunktion ist eine weitere periodische Funktion, die in der Signalverarbeitung häufig verwendet wird. Sie hat eine Periode \(T\) und oszilliert zwischen \(-1\) und \(1\), mit einem linearen Anstieg von von \(-1\) auf \(1\) und einem plötzlichen Abfall von \(1\) auf \(-1\).
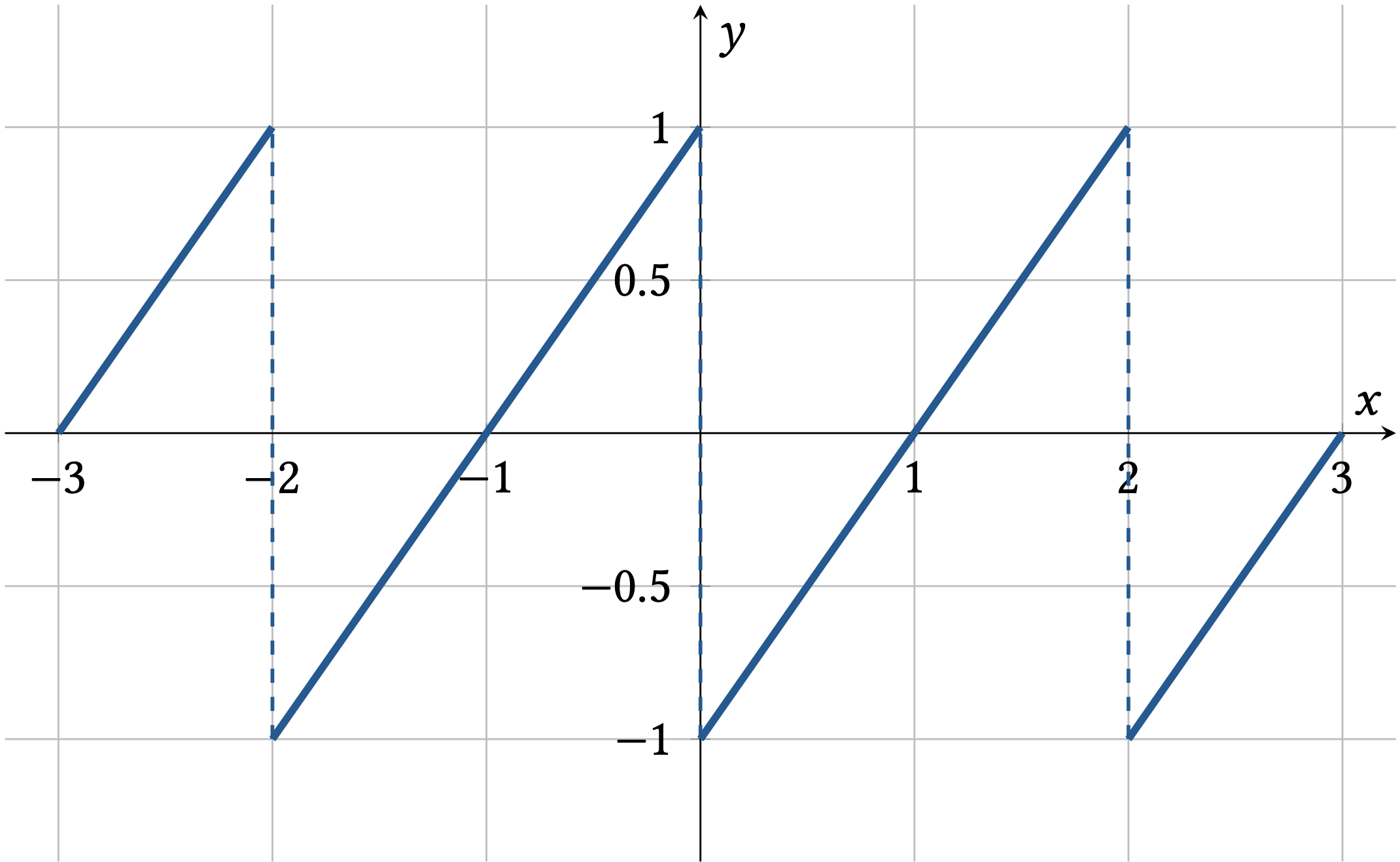
Fig. 7 Beispiel einer Sägezahnfunktion, die zwischen \(-1\) und \(1\) oszilliert und die Periode \(T = 2\) hat#
Zusammenfassung und Ausblick#
In diesem Kapitel haben wir gelernt, was periodische Funktionen sind. Wir haben zentrale Beispiele wie Sinus-, Kosinus-, Rechteck-, Dreieck- und Sägezahnfunktionen kennengelernt und gesehen, wie sie definiert sind und grafisch dargestellt werden. Im nächsten Kapitel werden wir uns mit der Annäherung von periodischen Funktionen durch die sogenannten Fourierreihen beschäftigen.