6.1 Definition und Visualisierung

6.1 Definition und Visualisierung#

Bisher haben wir nur Funktionen kennengelernt, bei denen eine reelle Zahl in die Funktionsvorschrift eingesetzt wurde und eine reelle Zahl herauskam. Die mathematische Schreibweise dafür ist \(f:\mathbb{R}\rightarrow\mathbb{R}\).

Allerdings ist die Welt nicht so eindimensional. Die folgende Abbildung zeigt beispielsweise die durchschnittliche Solarstrahlung in Deutschland. Dies ist mathematisch gesehen eine Funktion von mehreren Variablen, nämlich Längen- und Breitengrad, also \(f:\mathbb{R}^2\rightarrow\mathbb{R}\).

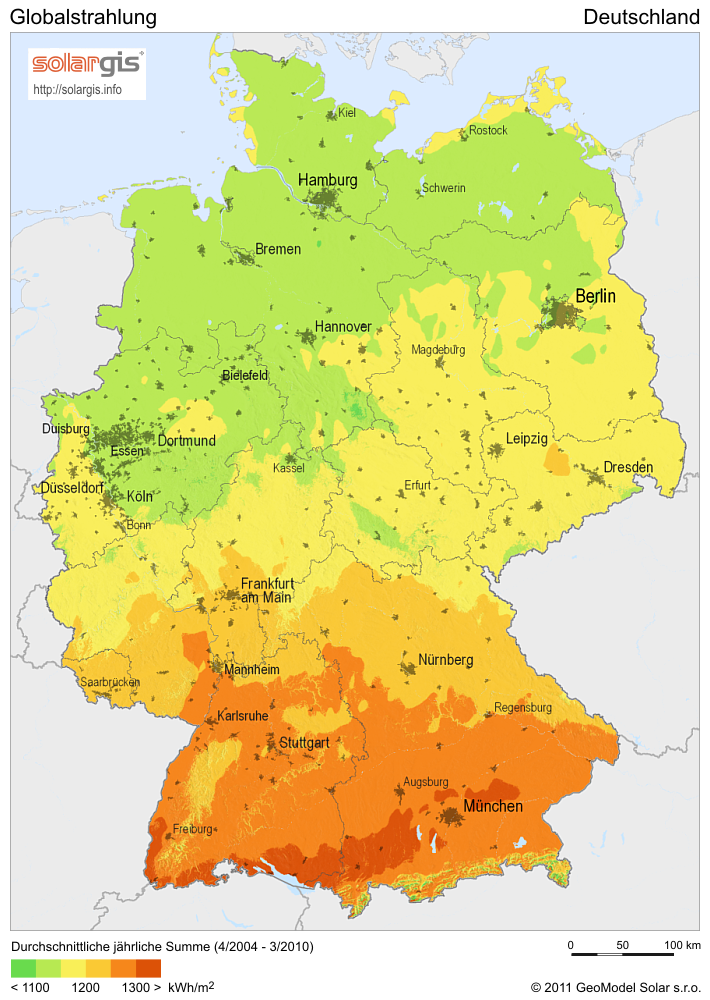
../_images/chapter06_fig01_solar_map.png — Fig. 13 Solarstrahlung in Deutschland#

(Quelle: “Solar Radiation Map: Globalstrahlung Deutschland, SolarGIS 2011”, Autor: SolarGIS Lizenz: CC BY-SA 3.0)

In diesem Kapitel werden wir uns Funktionen von mehreren unabhängigen Variablen genauer ansehen und insbesondere erarbeiten, wie solche Funktionen visualisiert werden können. Diese Art von Funktionen begegnet Ingenieuren im Maschinenbau täglich, zum Beispiel bei der Analyse von Temperaturverteilungen in Bauteilen.

Lernziele#

Lernziele

Sie können erklären, was eine Funktion von mehreren unabhängigen Variablen bzw. eine mehrdimensionale Funktion ist.
Sie können eine Funktion von zwei unabhängigen Variablen als Fläche im Raum zeichnen.
Sie können die Höhenlinien einer Funktion von zwei unabhängigen Variablen interpretieren und zeichnen.

Wiederholung: Begrifflichkeiten bei Funktionen#

Eine Funktion stellt eine Beziehung zwischen zwei Mengen her. Bei den bisher eingeführten Funktionen wird ein Element aus der sogenannten Definitionsmenge genommen und diesem genau ein Element aus der sogenannten Wertemenge zugeordnet. Wenn es darum geht, nun die Regeln dieser Beziehung genauer zu beschreiben, wird häufig eine Funktionsgleichung aufgestellt. Aber auch Tabellen oder grafische Abbildungen können dazu benutzt werden, um die Beziehung präzise zu beschreiben.

Als Beispiel einer Funktion betrachten wir eine Parabel. Als Definitionsmenge wählen wir alle reelle Zahlen, also alle Zahlen \(x\in\mathbb{R}\). Als Funktionsvorschrift legen wir nun fest, dass jedem \(x\) sein eigenes Quadrat zugeordnet wird, also in mathematischer Schreibweise

\[x\mapsto x^2.\]

Üblicherweise wird die Funktionsvorschrift als \(f(x)=x^2\) angegeben. Die grafische Darstellung sieht folgendermaßen aus:

../_images/chapter06_plot_parabel.svg — Fig. 14 Grafische Darstellung der Funktion \(f(x)=x^2\)#

Anhand der grafischen Darstellung wird schnell deutlich, dass zwar die Definitionsmenge alle reellen Zahlen umfasst, die Wertemenge jedoch nur die nichtnegativen reellen Zahlen enthält.

Funktionen von mehreren unabhängigen Variablen#

Nun betrachten wir ein Beispiel einer Funktion mit mehreren Eingabegrößen. Auch hier benötigen wir, um die Funktion zu beschreiben, eine Definitionsmenge, eine Wertemenge und eine eindeutige Zuordnungsregel. Während wir bisher Funktionen mit einer einzelnen Eingabegröße betrachtet haben, sollen nun mehrere Elemente der Definitionsmenge gemeinsam einem Element der Wertemenge zugeordnet werden. Die Elemente der Definitionsmenge werden auch unabhängige Variablen genannt, das Element der Wertemenge wird abhängige Variable genannt.

Ein typisches Beispiel aus dem Maschinenbau ist die Temperaturverteilung in einem Bauteil. Die Temperatur \(T\) an einem bestimmten Punkt hängt von den Raumkoordinaten \((x, y, z)\) ab, also \(T = f(x, y, z)\). Dies ist eine Funktion mit drei unabhängigen Variablen, die einem Punkt im Raum einen Temperaturwert zuordnet.

Für den einfacheren Fall mit zwei unabhängigen Variablen nennen wir diese \(x\) und \(y\) und legen fest, dass beides reelle Zahlen sind. Wir definieren nun eine Funktion, die jedem Wertepaar \((x,y)\) einen Funktionswert zuordnet.

Was ist … eine mehrdimensionale Funktion?

Eine mehrdimensionale Funktion \(f: \mathbb{R}^n \rightarrow \mathbb{R}\) ist eine Vorschrift, die jedem Punkt \((x_1, x_2, \ldots, x_n) \in \mathbb{R}^n\) aus der Definitionsmenge genau einen Wert \(f(x_1, x_2, \ldots, x_n) \in \mathbb{R}\) aus der Wertemenge zuordnet.

Als konkretes Beispiel betrachten wir die Funktion, die jedem Punkt \((x,y)\) die Summe der Quadrate zuordnet. Diese lässt sich in der mathematischen Notation auf zwei äquivalente Arten darstellen:

als Abbildungsvorschrift: \((x,y) \mapsto x^2 + y^2\) oder
als Funktionsgleichung: \(f(x,y) = x^2 + y^2\).

Die abhängige Variable \(z = f(x,y)\) kann nur Werte größer oder gleich Null annehmen, sodass die Wertemenge gleich \(\mathbb{R}_{0}^{+} = \{z \in \mathbb{R} \mid z \geq 0\}\) ist.

Das folgende Video erklärt mehrdimensionale Funktionen, wobei hier für mehrdimensional der Fachbegriff multivariat genutzt wird.

Darstellungen von Funktionen mit mehreren unabhängigen Variablen#

Für die Darstellung von mehrdimensionalen Funktionen gibt es verschiedene Möglichkeiten. Hier betrachten wir zwei Alternativen zur Darstellung von Funktionen \(f:\mathbb{R}^2 \rightarrow \mathbb{R}\), nämlich die 3D-Darstellung als Fläche im Raum und Höhenlinien.

3D-Darstellung als Fläche im Raum#

Um das obige Beispiel der Funktion \(f(x,y) = x^2 + y^2\) zu visualisieren, betrachten wir alle möglichen Kombinationen aus \(x\) und \(y\), d.h., die unabhängigen Variablen kommen aus der \(xy\)-Ebene. Zur Darstellung der abhängigen Variable \(z = f(x,y)\) benötigen wir eine dritte Dimension, die Höhe.

Die Funktion \(f(x,y) = x^2 + y^2\) beschreibt einen sogenannten Paraboloid, das folgendermaßen aussieht (Hinweis: Die Grafik ist interaktiv und kann durch Klicken und Ziehen gedreht werden):

Zusätzlich zur Höhe wurde die Paraboloid-Fläche gemäß der Funktionswerte \(f(x,y)\) eingefärbt. Die Farbskala rechts gibt an, welche Farbe welchem Funktionswert entspricht. Die Visualisierung von Funktionen mit mehr als zwei unabhängigen Variablen stellt eine Herausforderung dar, da wir nur drei räumliche Dimensionen zur grafischen Darstellung nutzen können. Es gibt jedoch alternative verschiedene Techniken, um mehrdimensionale Funktionen zu visualisieren, wie wir gleich sehen werden.

Höhenlinien#

Eine alternative Darstellung einer Funktion von zwei unabhängigen Variablen ist der sogenannte Contourplot oder das Konturliniendiagramm. Konturlinien sind auch aus dem Erdkundeunterricht bekannt, wo sie normalerweise Höhenlinien genannt werden.

Was sind … Höhenlinien?

Höhenlinien sind Linien in einer zweidimensionalen Ebene, die diejenigen Punkte \((x,y)\) verbinden, die den gleichen Funktionswert \(f(x,y)=c\) haben, wobei \(c\) eine Konstante ist.

Höhenlinien bieten eine zweidimensionale Darstellung einer dreidimensionalen Fläche. Liegen Höhenlinien eng beieinander, so ist die Steigung der Fläche in diesem Bereich steil; liegen sie weit auseinander, ist die Steigung flach.

Das folgende Beispiel zeigt die Höhenlinien der zuvor dargestellten Funktion \(f(x,y) = x^2 + y^2\), wobei die Definitionsmenge auf einen Kreis mit Radius \(r = 5\) zur besseren Visualisierung beschränkt ist:

Die kreisförmigen Höhenlinien in dieser Darstellung zeigen, dass die Funktion \(f(x,y) = x^2 + y^2\) für alle Punkte \((x,y)\) mit gleichem Abstand vom Ursprung denselben Wert annimmt. Dies entspricht dem rotationssymmetrischen Paraboloid, das wir in der 3D-Darstellung gesehen haben.

Das folgende Video erklärt den Contourplot.

Zusammenfassung und Ausblick#

In diesem Kapitel haben wir Funktionen mit mehreren unabhängigen Variablen kennengelernt. Wir haben gesehen, wie sich solche Funktionen mathematisch beschreiben lassen und wie sie visualisiert werden können, entweder als Fläche im dreidimensionalen Raum oder mithilfe von Höhenlinien in der Ebene. Im nächsten Kapitel werden wir uns mit der Stetigkeit von Funktionen mehrerer Variablen beschäftigen.