Übungen#
Übung 10.1
Berechnen Sie den Schwerpunkt des Dreiecks mit den Ecken \(P_1(2,5), \, P_2(6,2)\) und \(P_3(5,7)\). Machen Sie sich dazu eine Skizze des Integrationsgebietes.
Lösung
Fläche: \(A=\frac{17}{2}\), Schwerpunkt: \(S(\frac{13}{3}, \frac{14}{3})\)
Lösungsweg
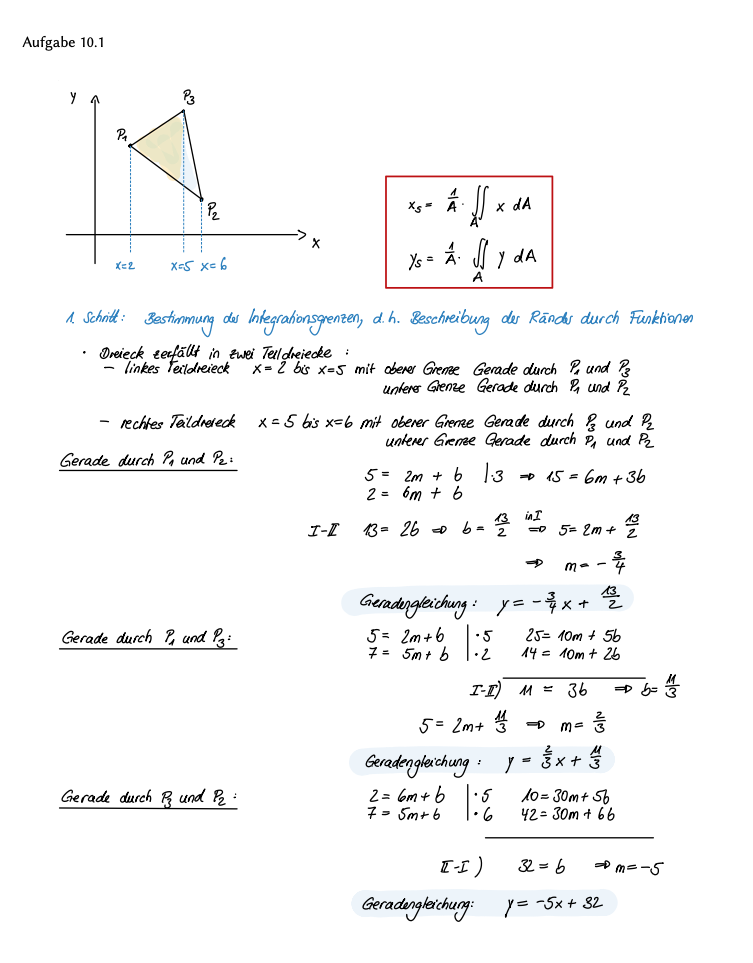


Übung 10.2
Berechnen Sie den Schwerpunkt eines Halbkreises mit Radius \(R=5\). Machen Sie sich dazu eine Skizze des Integrationsgebietes. Verwenden Sie Polarkoordinaten.
Lösung
Schwerpunkt: \(S(0, \frac{20}{3\pi})\)
Lösungsweg

Übung 10.3
Gegeben ist ein Prisma mit einer Länge von 2 cm (z-Richtung). Die dreieckige Querschnittsfläche sei gegeben durch die Punkte \((0,0), (1,0)\) und \((0,1)\) mit Einheiten in cm. Berechnen Sie den Schwerpunkt des Prismas.
Lösung
Volumen: \(V= 1 \text{cm}^3\), Schwerpunkt: \(S(\frac{1}{3}, \frac{1}{3}, 1)\) (in cm)
Lösungsweg
